In the world of Dichronauts, a vertical object that topples over in the wrong direction is in big trouble. If the gravitational up/down direction is “space-like”, then there will be both “space-like” and “time-like” horizontal directions, and if it’s possible to fall in a “space-like” direction then that will be no different from toppling over in our own world. That’s the safe way to fall. But we are interested in what happens if – for whatever reason – an object topples over in a direction of the opposite kind to up/down.
The geometry behind the scenarios discussed below is explained in more detail in the introductory page.
We will start with the simplest example possible. Suppose we have a tall, thin rod of uniform density that pivots at the bottom, so that when it topples, the lowest point of the rod stays fixed to the ground. Maybe it’s held in place by friction, or maybe it’s stuck partly into the ground; in any case, we are going to take it as given that however great a force is needed to hold the bottom of the rod in place, the ground will manage to provide that force. We will also assume that the rod itself remains undeformed and unbroken, whatever forces are applied to it.
You might be wondering why these caveats are necessary. After all, the rod is just falling over, it’s not gaining any extra weight. But in the Dichronauts universe, just as there are circumstances where an object sliding on a ramp can be subjected to forces from the ramp itself that are far greater than the weight of the object, it turns out that a toppling rod can be subjected to forces from the ground that far exceed its weight.
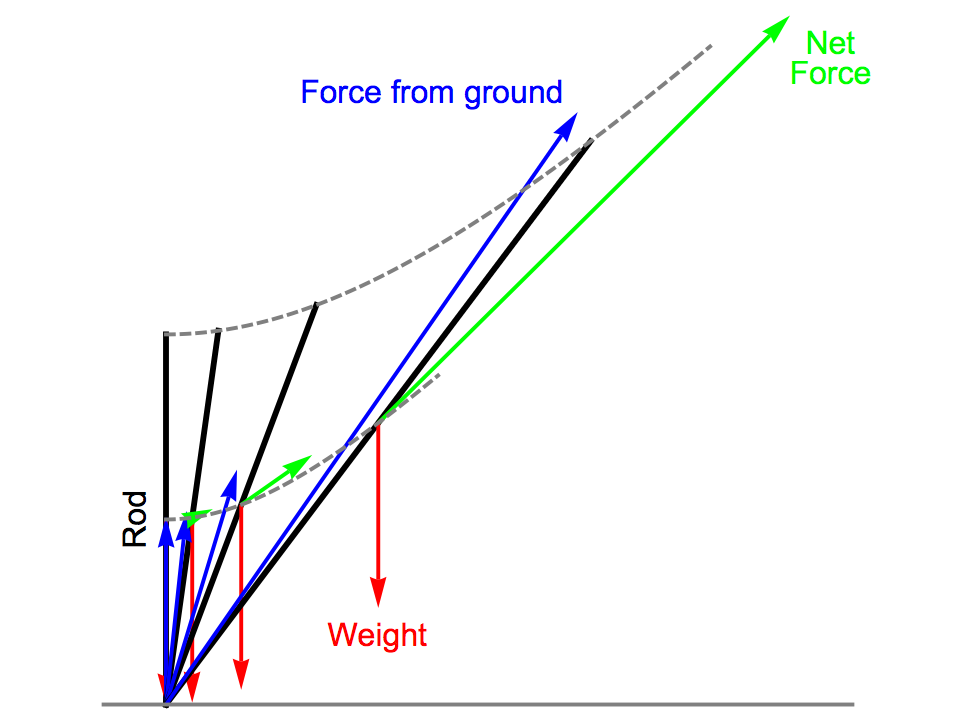
The image on the right shows a pivoting rod at four different moments, separated by equal time intervals. (We have given the rod a small push to get it started, otherwise, in theory, it could remain balanced vertically forever.)
As the rod topples over, both its top point and its centre of mass trace out hyperbolas (the dashed grey lines), as required for their distance from the fixed bottom point to remain constant in the Dichronauts geometry. The rate at which the rod topples can be found by conservation of energy: as the centre of mass rises higher, the rod gains potential energy, and this needs to be offset by a greater negative kinetic energy associated with motion in the time-like directions in which the elements of the rod are moving. So, the rod speeds up as it topples over.
From the path and speed of the centre of mass of the rod, we can deduce its acceleration, and hence the net force (green arrows) that must be applied to it. Note that the net force points roughly along the hyperbola followed by the centre of mass, but is not precisely a tangent to it, because the (hyperbolic) angular velocity of the rod is not constant. The only two forces acting on the rod are its weight (red arrows), which remains the same, and the force from the ground (blue arrows) keeping the bottom point still, which initially points upwards and simply opposes the weight, but increases, and takes on a horizontal component, as the rod topples over.
As the rod approaches a 45-degree slope, the force from the ground increases without limit. Of course it can never become literally infinite; the rod can never reach 45 degrees, and whatever it is made from, it will break at some point, or bend, or perhaps start slipping over the ground. But what this simple model demonstrates is that merely toppling over in the wrong direction has the potential to put an object under enormous stress, to the point where something has to give. And for one of the Walkers in the novel falling this way, the result would not be pleasant.
[The mathematical details are given in the supplementary page for this topic.]
Next, we will modify the situation from the previous example, and instead of having the bottom of the rod fixed, we will allow it to move freely across the ground, horizontally, with no friction at all. We will still assume that the rod remains perfectly straight and unbroken, and that the bottom is unable to penetrate the ground, but we will allow it to go sliding across this idealised, frictionless, infinitely tough but infinitely smooth, surface.
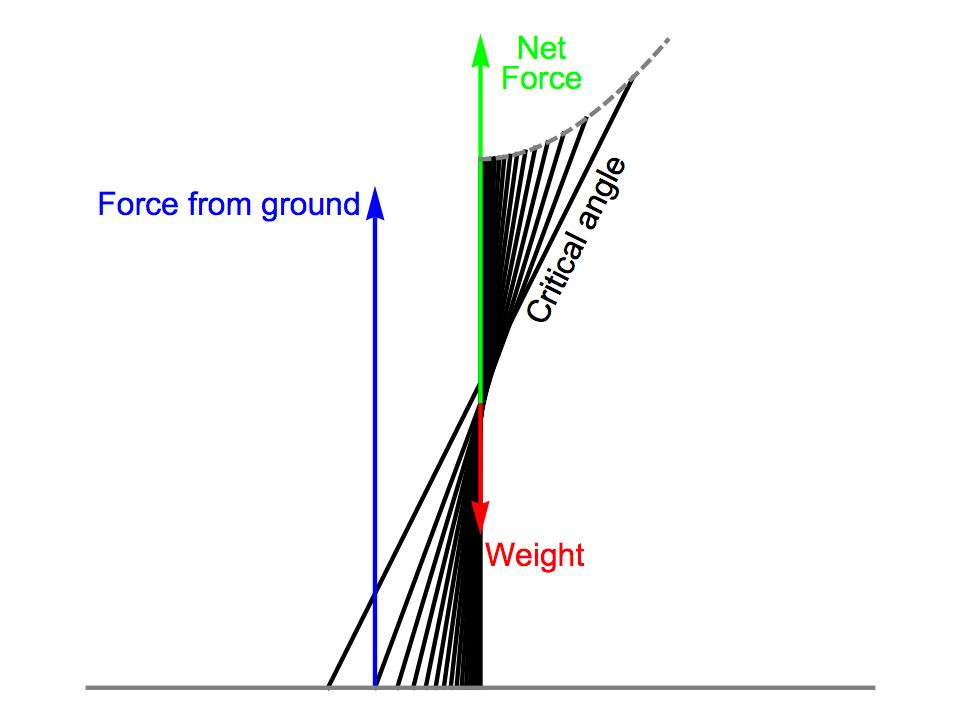
Once the rod starts to tip, its centre of mass will move in a purely vertical direction. What’s more, a growing region around the centre will move in directions that have larger vertical components than horizontal components, giving them “space-like” velocities. This portion of the rod will contribute positive amounts to the kinetic energy, and this positive contribution will grow, until, at a certain critical angle, it exactly balances the negative kinetic energy from the rest of the rod.
As the rod approaches that critical angle, the kinetic energy will be less and less sensitive to the rod’s angular velocity, which will need to increase without bound just to maintain a constant value of the total energy. So the motion will speed up, and the accompanying force required from the ground will also increase without bound.
The image on the right shows the rod at a sequence of positions separated by equal time intervals, with the last one placing the rod at the critical angle when the forces become infinite. The force vectors are drawn for the previous location in the sequence, when they would still be finite.
[The mathematical details are given in the supplementary page for this topic.]
Suppose we replace our idealised, infinitely strong rod with a tall, thin rectangular prism, and model it as a number of segments that will break apart if subjected to a sufficiently powerful shearing force.
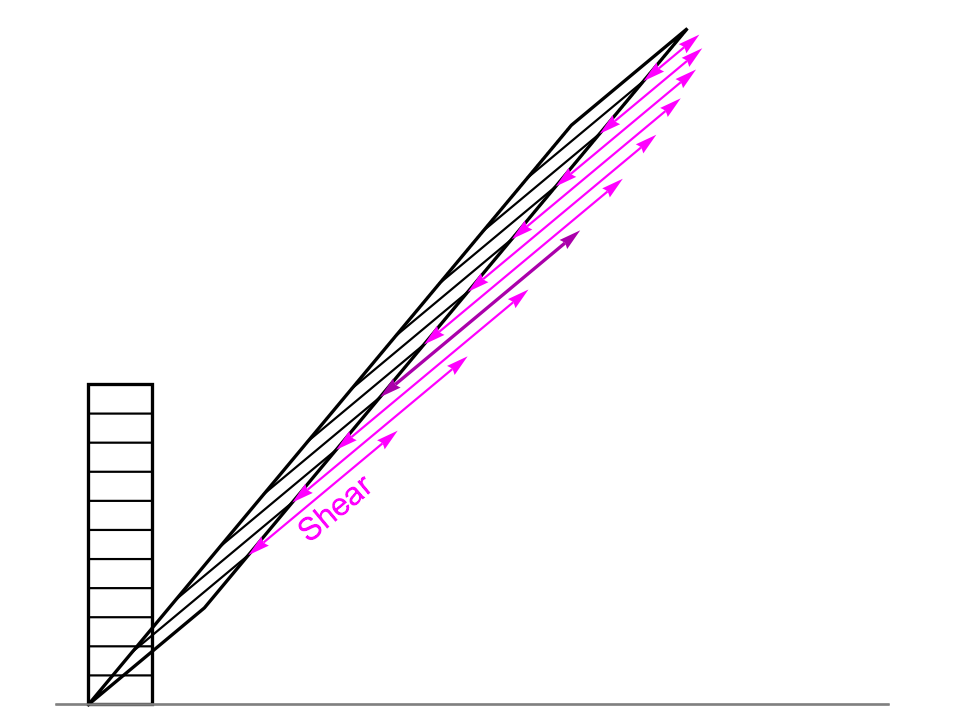
As before, we can use conservation of energy to calculate the speed at which the prism topples over while it remains intact, and so we can compute the acceleration of the centre of mass of each of these notional segments, and the force that must be applied, in addition to the segment’s own weight, to produce that acceleration.
The force on each segment will arise from equal and opposite forces exerted between each pair of adjoining segments (or in the case of the lowest segment, one of the forces will come from the ground). This gives us a list of linear equations to solve to determine the segment-to-segment forces, and once we have determined them, we can resolve them into normal forces acting perpendicular to the boundary, and shear forces acting along the boundary.
The image on the right illustrates the shear forces for a tilted prism. At this angle, they are greatest around 2/5 of the way up the prism, and they will increase without bound as the angle of tilt grows larger. So the material of the prism will eventually succumb to these forces, and it will shear into two or more pieces.
The breakup of the prism will be a complicated process, but these shorter pieces will end up tipping over, much like the original prism, and so they too will eventually shear apart. This will continue, until all the individual fragments are no longer taller than they are wide, making them stable when lying on the ground. However, as the pieces become shorter the point of maximum shear will move lower, and it will eventually lie close to the bottom of the prism. At that point, the ground will scrape off thin layers of material from the bottom, until the remainder of the prism becomes short enough that the process ceases.
[The mathematical details are given in the supplementary page for this topic.]