Orthogonal
Throughout these notes, we’ve adopted a system where time and distance are measured in identical units. This is the equivalent of setting the speed of light, c, equal to 1 in our own universe (for example, by measuring distances in metres and using the time it takes for light to travel one metre as the corresponding unit of time). In the Riemannian universe, it amounts to choosing units for time such that Pythagoras’s Theorem holds true, even when one side of the triangle involves an interval of time rather than space. In the novel Orthogonal, it is found empirically that this is the same as setting the speed of blue light equal to 1.
In this section, we will go one step further and choose units for mass and energy such that the “reduced Planck’s constant”, ℏ = h/(2π), is equal to 1. Mass and energy are then measured in units with the dimensions of inverse lengths or spatial frequencies — or, equally, inverse times or time frequencies.
Our particular choice means that the Planck relationship between frequency ν and energy, E = h ν, becomes E = 2 π ν = ω, where ω is the angular frequency of the wave, and the relationship between spatial frequency κ and momentum is p = 2 π κ = k, where k is the angular spatial frequency. The maximum angular frequency ωm that appears in the Riemannian Scalar Wave equation is then simply equal to the rest mass of the associated particle.
In the non-relativistic quantum mechanics we have discussed so far, we have simply applied the usual Schrödinger equation to the potential energy associated with the force between charged particles, on the basis that non-relativistic classical dynamics in the Riemannian universe is identical to Newtonian mechanics, so long as we treat kinetic energy as positive and choose the sign for the potential energy to be consistent with that.
For Riemannian relativistic quantum mechanics, we will need to do things slightly differently. The structure of quantum mechanics in its usual formulation is closely linked to the Hamiltonian form of the corresponding classical mechanics, and in the Riemannian case the momentum conjugate to each coordinate in the Hamiltonian sense is the opposite of the relativistic momentum in the same direction.
In non-relativistic quantum mechanics, we identify energy with the operator i ∂t, but we identify the spatial components of momentum with the operators –i ∂x, –i ∂y and –i ∂z. The same is true in Lorentzian relativistic quantum mechanics, but in the Riemannian case this makes no sense; we need to treat the space and time coordinates identically. In order to retain the usual correspondence with Hamiltonian classical mechanics, we will keep the identification:
E → i ∂t
and we will identify the relativistic momentum with the same kind of operators for the other coordinates, without the usual minus sign:
px → i ∂x
py → i ∂y
pz → i ∂z
This will also affect the operators we use for angular momentum. If we define the three-dimensional vector operator L = r × p using our Riemannian-relativistic momentum p, it becomes:
L = (x, y, z) × (i ∂x, i ∂y, i ∂z)
= i (y ∂z – z ∂y, z ∂x – x ∂z, x ∂y – y ∂x)
Like the linear momentum, this differs from the usual operator by a minus sign. As a result, the commutators between the components are different from those in non-relativistic quantum mechanics:
[Li, Lj] = –i εijk Lk
where the Levi-Civita symbol εijk is equal to 1 if (i, j, k) is an even permutation of (x, y, z), –1 if it is an odd permutation, and 0 if it contains any coordinate twice. Again, there is a difference of a sign in the right-hand side of this equation from the usual case.
Now, for the intrinsic angular momentum of particles to be compatible with this whole scheme, the corresponding operators need to have the same commutator algebra as the orbital angular momentum L. This means that rather than the Pauli spin matrices being the appropriate operators for the components of the angular momentum of a spin-½ particle, we will need to use the opposite of the Pauli matrices. The details will be developed as they arise; for now this is just a warning to expect this small twist on the usual conventions.
In our own universe, the Dirac equation is the relativistic wave equation that describes particles such as electrons and positrons: particles with mass, electric charge, and a spin of one half. The wave functions for these particles have four components, but they aren’t the components of a space-time vector, and they transform under the symmetries of the Lorentz group in a very different fashion to the way space-time vectors transform.
The corresponding equation for the Riemannian universe is extremely similar, and indeed it can be written in exactly the same form when expressed in terms of gamma matrices: a set of four matrices (each one of dimensions 4 × 4) that act on the wave function components. But the precise properties required of the gamma matrices are different in the two cases, reflecting the different signatures of the underlying space-time.
| Dirac Equation | |||||||||||||||||||
| m is the mass of the particle ψ is a four-component wave function I4 is the 4 × 4 identity matrix We’re using units such that ℏ = 1 | |||||||||||||||||||
| i γμ ∂μ ψ – m ψ | = | 0 | (Dirac Equation) | ||||||||||||||||
| {γμ, γν} | ≡ | γμ γν + γν γμ | |||||||||||||||||
| = | 2 gμν I4 | (Common) | |||||||||||||||||
| gμν | = | δμν | |||||||||||||||||
| = |
|
(Riemannian) | |||||||||||||||||
| gμν | = | ημν N.B.: (+ – – –) signature | |||||||||||||||||
| = |
|
(Lorentzian) | |||||||||||||||||
[For most of these notes we’ve used a positive sign for the spacelike dimensions in the Lorentzian case, giving a (– + + +) signature for η. But since virtually all quantum field theory literature uses a (+ – – –) signature, for ease of comparison we’ll switch to that convention.]
In the Dirac equation itself, we’re applying the Einstein Summation Convention to the index μ, which ranges over four space-time dimensions, combining each of the four gamma matrices with the derivative in the corresponding direction. The wave function ψ at any point in space-time is a four-component complex vector, with each gamma matrix acting on a derivative of ψ by ordinary matrix multiplication. But the four components of ψ are not indexed by the four space-time dimensions. We can write out the matrix multiplication explicitly with some extra indices for the relevant components (spinor indices, as opposed to space-time indices like μ):
i (γμ)sr ∂μ ψr – m ψs = 0
where the summation convention now applies to r as well as μ, and we explicitly have four equations, for the four values of the spinor index s.
Where we state the condition we’re imposing on the gamma matrices, the notation {γμ, γν} is known as an anticommutator. This is simply a convenient shorthand, using the definition:
{A, B} ≡ AB + BA
In defining the anticommutator A and B can be anything, but for our purposes they will usually be either matrices or other kinds of linear operators (such as differential operators). We will also make use shortly of the more familiar commutator notation:
[A, B] ≡ AB – BA
If ψ is a solution of the Riemannian Dirac equation, we will have:
i γμ ∂μ ψ – m ψ = 0
(i γμ ∂μ – m) ψ = 0
(–i γν ∂ν – m) (i γμ ∂μ – m) ψ = 0
(γν γμ ∂ν ∂μ + m2) ψ = 0
( ½(γμ γν + γν γμ) ∂ν ∂μ + m2) ψ = 0
(δνμ ∂ν ∂μ + m2) ψ = 0
The step between the third-last and second-last lines follows because, although the individual term γμ γν ≠ γν γμ, the sum over all such terms that we get from the summation convention is symmetrical under an exchange of μ and ν.
What the last line tells us is that each individual component of the four-component field ψ will obey the Riemannian Scalar Wave equation.
There are an infinite number of choices of gamma matrices that satisfy the condition {γμ, γν} = 2 δμν I4, since given any four matrices with this property we can always change to a different basis of C4, the four-complex-dimensional space on which these matrices act, and get four new matrices.
But certain choices for the gamma matrices make things simpler. We will give two examples, in what are known as the Weyl basis and the Dirac basis. First, it will be handy to remind ourselves of the Pauli spin matrices that appear in the quantum mechanics of angular momentum and rotations in three dimensions.
| Pauli spin matrices | |||||||
| σx | = |
|
|||||
| σy | = |
|
|||||
| σz | = |
|
(Common) | ||||
The commutators of half the Pauli matrices are:
[½σi, ½σj] = i εijk ½σk
What εijk does here is pick out the single value for k that is distinct from i and j, and select an appropriate sign, giving us:
[½σx, ½σy] = i ½σz
and cyclic permutations of this. As we discussed in the section on the Lie algebra so(3), the generators of rotations around the coordinate axes, Ji, have the commutator algebra:
[Ji, Jj] = εijk Jk
When describing the isomorphism between the Lie algebras su(2) and so(3), we used a basis {Hx, Hy, Hz} of su(2) comprised of three traceless skew-Hermitian matrices (matrices whose adjoint is the opposite of the original matrix). When doing quantum mechanics, it is more common to make use of Hermitian matrices, since any real-valued observable quantity in quantum mechanics has a Hermitian operator associated with it. The Pauli matrices are Hermitian matrices, related to our basis of su(2) by:
σk = i Hk
Hk = –i σk
Since the Hk are elements of su(2), any linear combination of them with real coefficients can be exponentiated to get an element of SU(2). The Hermitian matrices ½σk are the quantum-mechanical operators whose eigenvectors are states of definite spin, for a spin-½ particle in non-relativistic quantum mechanics; the corresponding eigenvalues are ±½. If we want to exponentiate a Hermitian matrix and end up with a unitary operator – an operator that preserves the norm of the quantum wave function – we need to multiply it by ±i first, e.g.:
Ux(θ) = exp(–i θ σx/2)
This is the unitary operator for a rotation by an angle θ around the x-axis, for a spin-½ particle in non-relativistic quantum mechanics.
When we shift from three dimensions to four, the Lie algebra so(4) has six generators Jμν for rotations in the six planes spanned by pairs of coordinate directions μ and ν. In order to fix the sign of the matrix Jμν, we use the convention that exponentiating a positive multiple of Jμν gives an element of SO(4) that rotates the μ axis towards the ν axis. The commutators of these generators are:
[Jμν, Jρν] = Jμρ
for the case where the two planes have exactly one coordinate axis, ν, in common. Apart from permutations of this with appropriate sign changes, all other commutators are zero. This makes sense, because if the two planes have no axes in common then rotations in them are completely independent, and if they have two axes in common then they are the same plane, and rotations in the same plane commute.
There is also a crucial change that we need to make when we switch from non-relativistic quantum mechanics to Riemannian relativistic quantum mechanics. Just as we need to use different operators than usual for linear momentum, we need to do the same for angular momentum. As we discussed earlier, for the orbital angular momentum this will happen automatically if we define it in terms of linear momentum, but for intrinsic angular momentum we need to choose the opposite of the usual Pauli matrices to get the correct sign for a particle’s spin. We’ll see a confirmation of this in the section on spin and conservation of angular momentum.
Our first choice for the Riemannian gamma matrices can be written in terms of the Pauli matrices as follows:
| Riemannian gamma matrices, Weyl basis | |||||||||
| γt | = |
|
= | σx ⊗ I2 | |||||
| γx | = |
|
= | σy ⊗ σx | |||||
| γy | = |
|
= | σy ⊗ σy | |||||
| γz | = |
|
= | σy ⊗ σz | |||||
| γμ | = |
|
(Riemannian) | ||||||
Here, the notation σx ⊗ I2 means we replace each entry in the first matrix, σx, by the product of that entry and the second matrix, I2, to get a 4 × 4 matrix. In the final line, we give a general form that applies for any index μ, if we use Ht = I2 as previously defined (but note that unlike the other three H matrices, Ht is not in su(2)).
All of these gamma matrices are Hermitian, traceless, and have a determinant of 1. The square of each matrix is the identity matrix, while all non-identical pairs anticommute: that is, their anticommutator is zero. If we compare these to the choice of gamma matrices in the Weyl basis used in Peskin and Schroeder’s widely used textbook on quantum field theory[1], our γt is the same, while the other matrices here are –i times the Lorentzian version. This reflects the fact that Peskin and Schroeder use a (+ – – –) signature for the metric, so their t coordinate already has a spacelike signature by our conventions.
We can use these gamma matrices to derive a representation of the group SO(4), using the formula from [1]:
Sμν = (i/4) [γμ, γν]
Here each Sμν is a Hermitian matrix that operates on the four-dimensional complex vector space to which the wave function ψ at each point belongs. It is the image of the so(4) element Jμν in some yet-to-be-determined four-dimensional Lie algebra representation, multiplied by a factor of ±i needed to make it Hermitian. And of course we’re not surprised to see the opposites of the Pauli matrices here, since we know that minus sign is going to be necessary to make the intrinsic spin compatible with everything else.
| Riemannian spin matrices, Weyl basis | |||||||||
| Sxy | = |
|
= | –½ I2 ⊗ σz | |||||
| Syz | = |
|
= | –½ I2 ⊗ σx | |||||
| Szx | = |
|
= | –½ I2 ⊗ σy | |||||
| Sxt | = |
|
= | ½ σz ⊗ σx | |||||
| Syt | = |
|
= | ½ σz ⊗ σy | |||||
| Szt | = |
|
= | ½ σz ⊗ σz | (Riemannian) | ||||
We can see from the fact that these matrices are block-diagonal that the four-dimensional representation they define is reducible: it can be split into two subspaces, each of two dimensions, that the action of the representation will never mix up.
What, then, are the two representations of so(4) that are stuck together here? By looking at the spin-(½,0) and spin-(0,½) representations that we previously described (and which is tabulated in detail at the end of that section), we see that the representation for the first two components of ψ corresponds to spin-(½,0), and the representation on the last two components matches spin-(0,½); the only difference is that the H matrices of su(2) in that discussion have been replaced by the opposites of the Pauli σ matrices.
The Lie algebra representation is just the derivative of the group representation, so the double cover of SO(4) should act on ψ via the group representation spin-(½,0) ⊕ spin-(0,½). And as we found when discussing representations that include parity, this can be extended to a representation of the double cover of O(4), in which the parity operation (reversing the signs of x, y and z) swaps the two 2-dimensional subspaces of this representation.
If we use ρ as an abbreviation for the spin-(½,0) ⊕ spin-(0,½) representation, then (up to a choice of sign, coming from the choice between two elements in the double cover of SO(4)) we have ρ:SO(4)→SU(4). That is to say, up to a sign, ρ assigns a 4 × 4 unitary matrix with determinant 1 to every rotation in SO(4). Readers familiar with the Dirac equation in the Lorentzian case will recall that the representation of “boosts” – coordinate changes that involve relative motion – in the analogous representation of SO(3,1) are not unitary, but in the Riemannian case we don’t face that complication.
Explicitly, ρ maps a rotation R in SO(4) to a unitary operator ρ(R) in SU(4) so that:
ρ(exp(Jμν)) = exp(i Sμν)
The derivative of this map is the Lie algebra isomorphism from so(4) to su(4):
dρ(Jμν) = i Sμν
Given this definition, it’s not too hard to verify that, for any rotation R in SO(4):
| ρ(R–1) γν ρ(R) | = | Rνζ γζ | (1) |
or if we spell out all the matrix multiplication here in index notation:
| ρ(R–1)qp (γν)pr ρ(R)rs | = | (Rνζ γζ)qs | (2) |
The easiest way to check this is to take the derivative, and use the formula (Jαβ)νζ = δαζ δβν – δαν δβζ:
| [γν, Sαβ] | = | –i (Jαβ)νζ γζ | |
| [γν, (i/4) [γα, γβ]] | = | i (δαν γβ – δβν γα) | |
| ¼ [γν, [γα, γβ]] | = | δαν γβ – δβν γα | |
| ¼ [γν, 2 δαβ I4 – 2 γβ γα] | = | ¼ ((γα γν + γν γα) γβ + γβ (γα γν + γν γα) – (γβ γν + γν γβ) γα – γα (γβ γν + γν γβ)) | |
| –½ (γν γβ γα – γβ γα γν) | = | ¼ (γν γα γβ + γβ γα γν – γν γβ γα – γα γβ γν) | |
| 0 | = | γν γα γβ + γν γβ γα – γα γβ γν – γβ γα γν | |
| 0 | = | γν (2 δαβ I4) – (2 δαβ I4) γν | |
| 0 | = | 0 |
Working backwards through these steps gives a derivation of the original claim.
What equations (1) and (2) tell us is that if we transform the spinor coordinates of the γ matrices using ρ(R), the result is the same as rotating the four γ matrices among themselves as if they were the components of a space-time vector acted on by the SO(4) element R.
The point of this is to understand what happens to the Dirac equation when we rotate our coordinates. If we make a change of coordinates from xμ to x'ν = Rνμ xμ, then the coordinate derivatives ∂μ are replaced by ∂'ν = (R–1)μν ∂μ, while our spinor wave function ψs is transformed into ψ'p = ρ(R)ps ψs. Writing the Dirac equation for everything in the new coordinates, we have:
| i (γν)pr ∂'ν ψ'r – m ψ'p | = | 0 | (3) |
Substituting for the transformed derivatives and wave function in terms of the originals:
| i (γν)pr (R–1)μν ∂μ ρ(R)rs ψs – m ρ(R)ps ψs | = | 0 | (4) |
Multiplying on the left by ρ(R–1) gives:
| ρ(R–1)qp [i (γν)pr (R–1)μν ∂μ ρ(R)rs ψs – m ρ(R)ps ψs] | = | 0 | |
| i ρ(R–1)qp (γν)pr (R–1)μν ∂μ ρ(R)rs ψs – m ρ(R–1)qp ρ(R)ps ψs | = | 0 | |
| i ρ(R–1)qp (γν)pr (R–1)μν ∂μ ρ(R)rs ψs – m ψq | = | 0 |
Making use of (2), this becomes:
| i (Rνζ γζ)qs (R–1)μν ∂μ ψs – m ψq | = | 0 | |
| i (γμ)qs ∂μ ψs – m ψq | = | 0 | (5) |
Equation (5) is the Dirac equation for the original ψ. So we’ve shown that the Dirac equation is SO(4)-invariant: the solutions we get if we rotate our coordinates with R are solutions of the original equation, transformed by ρ(R).
It’s worth stressing that when we transform ψ, we don’t treat the γ matrices as some kind of field that should itself be transformed. Rather, the gamma matrices bring together the space-time coordinate transformations of the derivatives and the corresponding spinor transformation of ψ in such a way that all the changes cancel out. The best way to think about the gamma matrices is as an intertwining operator, or intertwiner: a linear map from one vector space to another that commutes with representations of the same group on the two spaces. The terms ∂μ ψs transform under the tensor product of two representations of SO(4): the dual of the fundamental vector representation due to the space-time coordinate derivatives, and the spin-(½,0) ⊕ spin-(0,½) Dirac spinor representation. By multiplying both sides of equation (2) with (R–1)μν ρ(R)wq, rearranging the order of some terms (which we can do freely here, because the fully indexed terms are just scalars) and then applying both sides of the result to ∂μ ψs, we get:
| (γν)wr ρ(R)rs (R–1)μν ∂μ ψs | = | ρ(R)wq (γμ)qs ∂μ ψs | (6) |
On the right-hand side, γ maps a term in the tensor product, ∂μ ψs, to a Dirac spinor with index q, then ρ(R) acts on that to give another Dirac spinor, with index w. On the left-hand side, R–1 acts on the dual coordinate index μ while ρ(R) acts on the spinor coordinate s, and then γ takes the result (which at this point is still in the tensor product space) and maps it to a Dirac spinor with index w. That we can apply the representations either before or after using the map γ and get exactly the same result is what we mean by saying that γ is an intertwiner.
We chose the Weyl basis for the gamma matrices in order to make it as easy as possible to see which representation of SO(4) applied to ψ. Another basis, which will be useful in the next section, is the Dirac basis. In this basis, only γt changes, with all the other matrices exactly the same as in the Weyl basis.
| Riemannian gamma matrices, Dirac basis | |||||||||
| γt | = |
|
= | σz ⊗ I2 | |||||
| γx | = |
|
= | σy ⊗ σx | |||||
| γy | = |
|
= | σy ⊗ σy | |||||
| γz | = |
|
= | σy ⊗ σz | (Riemannian) | ||||
The resulting spin matrices are unchanged when only spatial coordinates are involved, so again they are block-diagonal, but the matrices that generate rotations involving the t coordinate mix the two halves of the spinor. This doesn’t mean that the representation of SO(4) has changed. The representation in the Dirac basis is equivalent to the representation in the Weyl basis.
| Riemannian spin matrices, Dirac basis | |||||||||
| Sxy | = |
|
= | –½ I2 ⊗ σz | |||||
| Syz | = |
|
= | –½ I2 ⊗ σx | |||||
| Szx | = |
|
= | –½ I2 ⊗ σy | |||||
| Sxt | = |
|
= | –½ σx ⊗ σx | |||||
| Syt | = |
|
= | –½ σx ⊗ σy | |||||
| Szt | = |
|
= | –½ σx ⊗ σz | (Riemannian) | ||||
Suppose we look for plane-wave solutions of the Dirac equation, of the form:
ψ(x) = u exp(–i k · x)
Here x is the coordinate four-vector. With our choice of units the propagation vector k is exactly the same as the energy-momentum vector associated with the plane wave, and of course |k| = m. The spinor u is a constant element of C4.
The Dirac equation then becomes a linear equation for u:
(kμ γμ – m I4) u = 0
So long as |k| = m the matrix here always has a determinant of 0, so there will always be non-trivial solutions. The easiest way to find a solution is to set k = m et, the energy-momentum vector of a stationary wave. In the Dirac basis this gives us:
|
= | 0 |
This is solved by any spinor with the last two components equal to zero, say:
u0 = (ξ, 0)
where we’re writing ξ for an arbitrary element of C2, and the 0 here is also to be taken as being in C2.
If we transform our coordinates in the zt plane with the SO(4) matrix exp(–θ Jzt), in the new coordinates the original vector m et will become the energy-momentum vector of a wave moving in the positive z direction with a velocity of tan θ. To find the spinor that accompanies this, we multiply u0 by exp(–i θ Szt).
k = exp(–θ Jzt) m et = m (cos θ et + sin θ ez)
u(k) = exp(–i θ Szt) u0 = (ξ cos(θ/2), i σz ξ sin(θ/2))
As the plane wave moves more rapidly, the first half of the Dirac spinor shrinks and the second half grows. At infinite velocity, θ=π/2, the two halves have equal magnitude.
Now, it’s tempting to assume that we can simply rotate beyond θ=π/2 to obtain a description of a Riemannian electron being transformed into a Riemannian positron by a change of coordinates, but the Dirac equation can’t quite deal with that. The problem is that a plane wave with a propagation vector pointing backwards in time would give us a negative energy, whereas we ought to measure a positive energy for a positron, just as we do for an electron. To deal correctly with the relationship between particles and antiparticles, we really need the more sophisticated formalism of quantum field theory.
What happens if we switch to the Weyl basis? We’ll look for solutions of the form:
ψ(x) = (ξL, ξR) exp(–i k · x)
When we substitute this into the Dirac equation, the resulting linear equation for ξL and ξR is:
(kμ γμ – m I4) (ξL, ξR) = 0
which, using the Weyl basis form of the gamma matrices expressed in terms of H matrices, we can write as:
kμ Hμ ξR – m ξL = 0
kμ Hμ* ξL – m ξR = 0
As we’d expect from what we saw in the Dirac basis, these equations are not independent. Since kμ Hμ is |k| times a unitary matrix (i.e. a matrix whose inverse is its Hermitian adjoint), we have:
(kμ Hμ)(kμ Hμ*) = |k|2 I2 = m2 I2
So if we multiply the second of our matrix Dirac equations on the left with kμ Hμ, then divide through by m, we obtain the first equation again.
For a stationary particle, with k = m et, solutions take the form:
ψ(x) = (ξ, ξ) exp(–i m t)
If we boost this in the zt plane – using the Weyl basis spin matrices, of course – we have:
k = exp(–θ Jzt) m et = m (cos θ et + sin θ ez)
(ξL, ξR) = exp(–i θ Szt) (ξ, ξ) = (exp(–½i θ σz) ξ, exp(½i θ σz) ξ)
The matrices exp(±½i θ σz) are diagonal, with entries equal to the phases exp(±½i θ), so unlike the case with the Dirac basis the norms of each half of the spinor are unchanged by the boost.
In the Weyl basis, we can easily construct a plane wave solution for any value of k:
(ξL(k), ξR(k)) = (√[(kμ Hμ)/m] ξ, √[(kμ Hμ*)/m] ξ)
Substituting this into the first of the matrix Dirac equations, kμ Hμ ξR – m ξL = 0, and multiplying through by √m gives:
kμ Hμ √[kμ Hμ*] ξ – m √[kμ Hμ] ξ = 0
√[kμ Hμ] √[(kμ Hμ)(kμ Hμ*)] ξ – m √[kμ Hμ] ξ = 0
m √[kμ Hμ] ξ – m √[kμ Hμ] ξ = 0
which verifies that it is a solution. In case you’re groaning at the idea of having to take the square root of a matrix, we can actually describe this kind of square root quite easily:
√[kμ Hμ] = (kμ Hμ + m Ht) / √[2(m+kt)]
Suppose we pick an orthonormal basis {ξs} of C2. A useful example would be the normalised eigenvectors of one of the Pauli spin matrices – and by convention, the usual choice is σz, in which case we’d use the labels s=±½. We can then write a pair of normalised plane wave solutions of the Riemannian Dirac equation for any 4-momentum as:
| Plane Wave Solutions of the Riemannian Dirac Equation in the Weyl Basis | |||
| k is a 4-momentum, |k|=m {ξs} is an orthonormal basis of C2 Hμ are the unit quaternions as matrices (defined here) Sum kjHj ranges over spatial indices x, y, z. | |||
| ψk, s(x) | = | u(k, s) exp(–i k · x) | (Plane wave) |
| u(k, s) | = | ( [(m+kt)Ht + kjHj] ξs, [(m+kt)Ht – kjHj] ξs) / (2 √[m(m+kt)]) | (4-spinor part) |
| u(k, s1)† u(k, s2) | = | ξs1† ξs2 | |
| = | δs1, s2 | (Orthonormality) | |
Now, if we pursue the results of the previous section describing plane waves in the Weyl basis, and identify both the space H of 2×2 complex matrices spanned by the Hμ and the two-complex-dimensional space C2 with the quaternions, as we previously described, we can take the first equation between the spinors ξL and ξR and the energy-momentum vector k as an equation between three quaternions:
kμ Hμ ξR – m ξL = 0
→
QV qR – m qL = 0
where QV = kμ Hμ is a quaternion that transforms as a vector, qL is a quaternion that transforms as a left-handed spinor, and qR is a quaternion that transforms as a right-handed spinor. In other words, the action of an element (g, h) of SU(2)×SU(2) on these three quaternions is given by:
ρ(½, ½)(g, h) QV = g QV h–1
ρ(½, 0)(g, h) qL = g qL
ρ(0, ½)(g, h) qR = h qR
The product QV qR transforms in the same way as qL, making the equation invariant. Following our previous discussion, if we choose a unit vector v0 in C2 we can explicitly indentify ξL = qL v0 and ξR = qR v0. In that case, multiplying our quaternion equation on the right with v0 gives the corresponding spinor equation.
So we see that the Dirac equation for a plane wave can be interpreted as giving an extremely simple linear relationship between three quaternions that transform under different representations of SU(2)×SU(2), with a vector for the energy-momentum of the particle, and a pair of left- and right-handed spinors for the wave itself.
| Riemannian Dirac Equation for Quaternions | |||
| (qL, qR) is Dirac spinor as a pair of quaternions QV is the energy-momentum vector of a plane wave solution: ψ(x) = (qL, qR) exp(–i QV · x) | |||
| QV qR – m qL | = | 0 | (Riemannian) |
To understand this quaternionic description better, let’s look at how the usual two-component spinor version of the angular momentum of a spin-½ particle can be translated into quaternionic terms. We first have to choose a complex structure: a linear operator J on H that corresponds to multiplication by i on C2. Squaring J must amount to multiplication by –1, and J should commute with any linear operators on H that correspond to complex-linear operators on C2. We can achieve these requirements by making J equal to right-multiplication by some quaternion that is a square root of –1, and implementing other linear operators as left-multiplication. To be concrete, let’s choose:
J(q) = q Hz
Given this choice, we set v0=(0,1), an eigenvector of Hz with eigenvalue i. We then identify H and C2 via T:H→C2, where
T(q) = q v0
T(J(q)) = q Hz (0, 1) = i q (0, 1) = i T(q)
The choice of J identifies two planes in H that we can think of as the complex planes of the two components of the usual spinor: the zt plane and the xy plane. Multiplication of a quaternion q by any complex number a + b i (where a and b are real) is implemented as right-multiplication by a + b Hz, and this operation maps both of these planes into themselves.
We give H the spinor inner product < >S:
< p, q >S = ReH(p* q) – ReH(p* J(q)) i = ReH(p* q) – ReH(p* q Hz) i
where “ReH” means the real part of a quaternion, as distinct from the real part of a complex number, which we’ll write “ReC”. We’ll use “*” to denote the conjugate of a quaternion, and “conj” to denote ordinary complex conjugation. If we represent the quaternions as 2×2 complex matrices, quaternionic conjugation is just taking the Hermitian adjoint or complex-conjugate-transpose of those matrices, so q* = conj(qT).
Our spinor inner product is really just the standard inner product on C2 transferred to H, so that:
< p, q >S = < T(p), T(q) >
To see this, start with the real part:
ReC < T(p), T(q) > = ½(< T(p), T(q) > + < T(q), T(p) >)
= ½(< p v0, q v0 > + < q v0, p v0 >)
= ½(< v0, p* q v0 > + < v0, q* p v0 >)
= < v0, ½(p* q + q* p) v0 >
= ReH(p* q) < v0, v0 >
= ReH(p* q)
We get from the third-last line to the second-last because ½(p* q + q* p) = ReH(p* q) is just a pure real number – or, in terms of matrices, the same real number times the 2×2 identity matrix. For the imaginary part:
ImC < T(p), T(q) > = ReC(–i < T(p), T(q) >) i
= – ReC(< T(p), i T(q) >) i
= – ReC(< T(p), T(q Hz) >) i
= – ReH(p* q Hz) i
Now, the usual spin eigenstates ξk± in the two-component spinor formalism obey the equations (for k=x, y, z):
–σk ξk± = ±ξk±
Note that we’ve used the opposite of the Pauli matrices here, for reasons we discussed previously. In the quaternion formalism, we need to replace the Pauli matrices σk (which aren’t elements of H) with the basis quaternions Hk = –i σk and replace the C2 spinors ξk± with the quaternion spinors qk± that satisfy ξk± = qk± v0. This leads us to the quaternion equations:
Hk qk± = ±qk± Hz
If we multiply this equation by –i, multiply v0 by each side, and use the fact that v0 is an eigenvector of Hz with eigenvalue i, we recover the previous equation for spinors in C2.
The solutions to these quaternion equations are entire planes in H for each choice of sign, though of course they are planes that are mapped into themselves by multiplication with any complex number, corresponding to one-complex-dimensional eigenspaces in C2.
For Hx, the positive eigenspace is spanned by Ht+Hy and Hx+Hz; the negative eigenspace is spanned by Ht–Hy and Hx–Hz.
For Hy, the positive eigenspace is spanned by Ht–Hx and Hy+Hz; the negative eigenspace is spanned by Ht+Hx and Hy–Hz.
For Hz, the positive eigenspace is spanned by Ht and Hz; the negative eigenspace is spanned by Hx and Hy.
(All of this extends to the left- and right-handed spinor representations of the double cover of SO(4), where we measure spins in various coordinate planes in R4. The various spin operators are all (half) H matrices or their opposites, as listed at the end of this section, so we can get everything we need from the eigenspaces described above. For example, spin in the zt coordinate plane for the spin-(½,0) left-handed spinor representation is measured by –½ Hz, so its positive and negative eigenspaces are just the negative and positive eigenspaces of Hz described above.)
Any spinor in C2 will be the positive spin eigenstate of the spin measured along some direction in space. In the quaternion formalism, this direction for a quaternion q is very easy to describe. For our choice of complex structure, it’s simply:
s(q) = q Hz q–1
Obviously this satisfies:
s(q) q = q Hz
The spin axis s(q) will always be a purely spatial vector, since Hz is spatial to begin with, and all rotations in SO(4) produced by ρ(½, ½)(g, g) QV = g QV g–1 leave the time axis unchanged, and so are actually rotations in SO(3). We can also very easily find a spinor quaternion whose spin is precisely the opposite of that of q, which we’ll call revS(q):
revS(q) = q Hy
s(revS(q)) = q Hy Hz Hy–1 q–1 = q Hy Hz (–Hy) q–1 = –q Hx Hy q–1 = –s(q)
The spin-reversal function revS is conjugate-linear according to our complex structure of right-multiplication by Hz:
revS(i q) = revS(q Hz) = q Hz Hy = –q Hy Hz = –i revS(q)
It’s easy to see that revS commutes with the action of SU(2)×SU(2), since that action multiplies quaternions on the left while revS multiplies them on the right.
Any rotation in SO(3) that leaves the vector s(q) fixed can be produced by ρ(½, ½)(g, g) with g = cos(θ) Ht + sin(θ) s(q). Such rotations will act on the spinor q (whether it’s left- or right-handed) by left-multiplication with g, giving:
g q = (cos(θ) Ht + sin(θ) s(q)) q
= (cos(θ) Ht + sin(θ) q Hz q–1) q
= cos(θ) q + sin(θ) q Hz
= (cos(θ) + i sin(θ)) q
= exp(i θ) q
In other words, the rotation merely changes the overall phase of the spinor q.
In a relativistic context where the particle can be in motion with some arbitrary velocity, we can no longer think of rotations as having an axis. Instead, we identify a rotation with a pair of unit quaternions (sL, sR), acting via v → sL v sR–1. If we make an arbitrary change of coordinates corresponding to a rotation (g, h), then our original rotation is transformed to (g sL g–1, h sR h–1). This comes from composing three operations: (1) inverting the coordinate change to take things back to the coordinates of the original rotation, (2) performing the original rotation, and (3) applying the coordinate change to return to the new coordinates.
If we have a particle whose state is the Dirac spinor (qL, qR) and qL≠0, qR≠0, we can define a pair of unit quaternions to use for a rotation:
sL(qL) = qL Hz qL–1
sR(qR) = qR Hz qR–1
Note that if we apply a change of coordinates corresponding to (g, h), and use the spinor transformation laws qL → g qL and qR → h qR, the rotation (sL(qL), sR(qR)) transforms exactly as a rotation should under coordinate changes. It also follows from these definitions that sL(qL)2 = sR(qR)2 = –Ht, so applying the rotation twice, v → sL(qL)2 v sR(qR)–2 just gives the identity transformation.
Clearly sL(qL) and sR(qR) will satisfy:
sL(qL) qL = qL Hz
sR(qR) qR = qR Hz
The physical meaning of this is that a rotation of vectors produced by the pair (sL(qL), sR(qR)) will be accompanied by a transformation of the Dirac spinor (qL, qR) → (sL(qL) qL, sR(qR) qR) = (qL Hz, qR Hz), which amounts merely to multiplying the whole Dirac spinor by i according to the complex structure we’ve put on H.
In a frame where the particle is at rest the energy-momentum vector QV will equal m Ht, so the equation:
QV qR – m qL = 0
will give us qR = qL, which in turn means sL(qL) = sR(qR), and the associated rotation will be three-dimensional. Because we know that the rotation squared is the identity, it must be a half-turn in a particular plane. That fact won’t change when we switch to a frame where the particle is in motion, so in general we can treat (sL(qL), sR(qR)) as identifying a plane of rotation associated with the particle’s spin, in place of the spin axis s(q) used in the three-dimensional context.
What’s more, we can identify two vectors orthogonal to the plane (and to each other) that will be unchanged by the rotation: the energy-momentum vector QV = m qL qR–1, and the vector:
sLR(qL, qR) = qL Hz qR–1
The latter coincides with the spin axis s(q) when the particle is stationary and qR = qL.
If we apply the spin-reversal function revS to both quaternions in a Dirac spinor, all four quaternions related to the spin geometry are reversed: sL(qL), sR(qR), QV and sLR(qL, qR).
It’s easy to construct a Lagrangian that yields the Riemannian Dirac equation:
| Lagrangian for Dirac Equation | |||
| LRD | = | ψ† (i γμ ∂μ ψ – m ψ) | |
| = | i ψ† γμ ∂μ ψ – m ψ†ψ | (Riemannian) | |
| LLD | = | ψ† γt (i γμ ∂μ ψ – m ψ) | |
| = | i ψ† γt γμ ∂μ ψ – m ψ† γt ψ | (Lorentzian) | |
Here ψ† is the Hermitian adjoint, or conjugate transpose, of the 4 × 1 column vector ψ, so it is a 1 × 4 row vector that we multiply into the objects on its right by matrix multiplication.
In the Lorentzian case, the matrices that represent Lorentz transformations on ψ are generally not unitary, and as a consequence ψ†ψ is not a scalar: it is not invariant under Lorentz transformations. So it’s necessary to replace ψ† by ψ† γt; this gives a Lorentz-invariant inner product, ψ† γt ψ, and allows a Lorentz-invariant Lagrangian to be constructed. (In the QFT literature, ψ† γt is abbreviated as ψ with a bar over the top.) But those minor headaches belong solely to the Lorentzian case. In the Riemannian case, all the spin matrices are Hermitian, the representation of SO(4) is unitary, and ψ†ψ is SO(4)-invariant:
ψ → U ψ
ψ† → (U ψ)† = ψ† U† = ψ† U–1
ψ†ψ → ψ† U–1 U ψ = ψ†ψ
The first term of LRD is also SO(4)-invariant, as can easily be shown with the help of equation (2) from the section on gamma matrices.
We obtain the Dirac equation from the Lagrangian by means of the Euler-Lagrange equations. We treat ψ† as an independent field, and write:
∂μ [ ∂∂μ ψ†LRD ] = ∂ψ†LRD
0 = i γμ ∂μ ψ – m ψ
where the expression in square brackets is zero because the Lagrangian doesn’t depend on any derivative of ψ†. The corresponding calculation using ψ itself as the field gives the same answer, merely with more work:
∂μ [ ∂∂μ ψLRD ] = ∂ψLRD
∂μ [ i ψ† γμ ] = –m ψ†
i ∂μ ψ† γμ + m ψ† = 0
–(i ∂μ ψ† γμ + m ψ†)† = 0
i γμ ∂μ ψ – m ψ = 0
Now that we have the Lagrangian for the Dirac equation, we can use Noether’s Theorem to identify a conserved current. Suppose we multiply our Dirac spinor ψ by any unit-magnitude complex number, also known as a “phase”: exp(i α) for a real-valued α. Since ψ† ends up with the opposite phase, the Lagrangian is unchanged.
Noether’s Theorem associates a conserved current with every such symmetry of the Lagrangian:
jμ = (∂∂μ ψLRD) (∂α exp(i α) ψ)|α=0
= –ψ† γμ ψ
We can multiply this by any constant and the current will still be conserved. Specifically, we’ll define:
| Current for Dirac Equation | |||
| e is charge on particle | |||
| jμ | = | e ψ† γμ ψ | (Riemannian) |
| jμ | = | e ψ† γt γμ ψ | (Lorentzian) |
What we mean by calling this a “conserved current” is that its divergence is zero, so it doesn’t appear or disappear out of thin air.
∂μ jμ = e ∂μ (ψ† γμ ψ)
= e ((∂μ ψ†) γμ ψ + ψ† γμ (∂μ ψ))
= e ((i m ψ†) ψ + ψ† (–i m ψ))
= 0
Consider the stationary plane wave solution, using the Dirac basis:
ψ(x) = (ξ, 0) exp(–i m et · x)
where ξ is any two-component spinor. For this solution, we have simply:
j = e (ξ†ξ) et
because the structure of the gamma matrices apart from γt makes all the other components zero. Of course with an infinite plane wave we face the usual problems of normalisation, but we’ll ignore that for now and just focus on the direction of j, which is aligned with the particle’s propagation vector in this particular case – and will continue to be aligned if we switch to a reference frame in which the wave is moving. So j behaves just as we’d expect for an electric current density.
We can combine the Lagrangian for the Dirac equation with that we previously derived for the Riemannian Proca equation, the equation governing electromagnetism. We can then make use of our expression for the current density in terms of the Dirac field, to give a total Lagrangian expressed entirely in terms of the elementary fields. [Note that for the Lorentzian versions we’re using a (+ – – –) signature on this page, for ease of comparison with QFT textbooks. This means that some of these Lorentzian equations are not quite what you’d expect from the versions in the notes on electromagnetism.]
| Lagrangian for Quantum Electrodynamics | |||
| mph is the mass of the photon m is the mass of the Dirac particle and e is its charge Electromagnetic field Fμν = ∂μ Aν – ∂ν Aμ | |||
| LRQED | = | ψ† (i γμ ∂μ ψ – m ψ) + ¼ FμνFμν – ½ mph2 Aμ Aμ – Aμ jμ | |
| = | ψ† (i γμ ∂μ ψ – m ψ) + ¼ FμνFμν – ½ mph2 Aμ Aμ – e Aμ ψ† γμ ψ | (Riemannian) | |
| LLQED | = | ψ† γt (i γμ ∂μ ψ – m ψ) – ¼ FμνFμν – Aμ jμ | |
| = | ψ† γt (i γμ ∂μ ψ – m ψ) – ¼ FμνFμν – e Aμ ψ† γt γμ ψ | (Lorentzian) | |
The Euler-Lagrange equations for these Lagrangians give us both the equation for the electromagnetic field coupled to the Dirac source, and the Dirac equation in the presence of an electromagnetic field.
| Field Equations for Quantum Electrodynamics | |||
| mph is the mass of the photon m is the mass of the Dirac particle and e is its charge Electromagnetic field Fμν = ∂μ Aν – ∂ν Aμ | |||
| ∂μ∂μ Aν + mph2 Aν + e ψ† γν ψ | = | 0 | |
| i γμ ∂μ ψ – m ψ – e Aμ γμ ψ | = | 0 | (Riemannian) |
| ∂μ Fμν – e ψ† γt γν ψ | = | 0 | |
| i γμ ∂μ ψ – m ψ – e Aμ γμ ψ | = | 0 | (Lorentzian) |
The Riemannian Dirac equation in an electromagnetic field is:
i γμ ∂μ ψ – m ψ – e Aμ γμ ψ = 0
Let’s rewrite this in an explicitly Hamiltonian form, by multiplying through on the left by γt (whose square, like that of all the Riemannian gamma matrices, is the identity matrix) and separating out the time derivative:
i ∂t ψ = H ψ
H = –i γt γj ∂j + m γt + e Aμ γt γμ
Here the sum over the repeated index j covers spatial coordinates only, while the sum over μ covers all four dimensions.
We will call the gamma matrices multiplied on the left by γt the alpha matrices, and like the gamma matrices they take a very simple form in the Weyl basis:
| Riemannian alpha matrices, Weyl basis | |||||||
| αμ | = | γt γμ | |||||
| = |
|
(Riemannian) | |||||
Now, an operator for an observable will describe a conserved quantity if it commutes with the Hamiltonian. If we have a Riemannian electron in a radially symmetric electrostatic field we would expect its angular momentum to be conserved, so let’s compute the commutator between the Hamiltonian for that situation and the orbital angular momentum operator L = r × p. In an electrostatic field with potential V(r) we have At = –V(r), while all other Aj = 0, giving us a Hamiltonian:
H = –i αj ∂j + m γt – e V(r)
= – αj pj + m γt – e V(r)
where pj = i ∂j is the jth component of the linear momentum; don’t forget that we have to use a different convention for the operator for Riemannian relativistic momentum. The orbital angular momentum operator has components:
Li = εijk xj pk
To find its commutator with the Hamiltonian, we first compute:
[xj pk, ps] = –[xj ∂k, ∂s]
= –( xj ∂k ∂s – ∂s(xj ∂k) )
= –( xj ∂k ∂s – xj ∂s ∂k – δsj ∂k )
= –i δsj pk
This gives us:
[Li, ps] = –i εisk pk
Li will clearly commute with the second term in the Hamiltonian, which involves only multiplication by a fixed matrix. What about the third term? For any function f that depends solely on the squared radial distance r2 = x2 + y2 + z2 = xl xl, and any function g we have:
[xj pk, f(xl xl)] g = i [xj ∂k, f(xl xl)] g
= i ( xj ∂k ( f(xl xl) g ) – f(xl xl) xj ∂k g )
= i ( 2 g xj xk f '(xl xl) + f(xl xl) xj ∂k g – f(xl xl) xj ∂k g )
= 2 i xj xk f '(xl xl) g
Writing the result as a linear operator without the function g:
[xj pk, f(xl xl)] = 2 i xj xk f '(xl xl)
Since this expression is symmetric in the indices j and k, the antisymmetric ε in Li = εijk xj pk will give a total of zero for [Li, f(xl xl)], and since the third term in the Hamiltonian can be expressed as a function with the form of f, that term will commute with Li.
That leaves only the first term in the Hamiltonian. So we have:
[Li, H] = [Li, – αj pj]
= – αj [Li, pj]
= i εijk αj pk
Since this is non-zero, orbital angular momentum will not be conserved. However, if we attribute spin angular momentum to the electron itself in the right manner, total angular momentum can still be conserved.
We previously described the Hermitian spin matrices Sμν that represent the generators of rotations. If we define the spatial spin matrices S = (Syz, Szx, Sxy), in the Weyl basis we have Si = –½ I2 ⊗ σi = –½ i I2 ⊗ Hi.
| Spatial spin matrices, Weyl basis | |||||||
| Si | = |
|
(Riemannian) | ||||
The commutators of the H matrices with spatial indices are:
[Hj, Hk] = 2 εjkl Hl
Now in the alpha matrices with spatial indices, the adjoint matrix Hj* = –Hj. From this, we can easily compute the commutators of the spatial spin matrices with spatial alpha matrices:
[Si, αj] = –i εijl αl
The matrix Si will commute with all but the first term of the Hamiltonian, and so:
[Si, H] = – [Si, αj] pj
= i εijl αl pj
= i εikj αj pk [Relabelling indices]
= –i εijk αj pk
This is the opposite of the commutator with the orbital angular momentum component Li, so we have, for the total angular momentum:
[L+S, H] = 0
The fact that we have ended up with a conserved quantity for the total angular momentum confirms that we have made the correct choice for the spin matrices!
We previously discussed how pairs of quaternions (qL, qR) could be interpreted as Dirac spinors, and how the angular momentum of a spin-½ particle could be described in that formalism. We treat each copy of the quaternions as a two-complex-dimensional Hilbert space, in place of the usual spinor space C2, by giving it a complex structure – and our particular choice was to use multiplication on the right by the quaternion Hz as multiplication by i, the square root of minus 1. With these conventions, the Dirac equation for a free plane wave in the Weyl basis becomes extraordinarily simple:
qV qR – m qL = 0
Here (qL, qR) is the Dirac spinor, with the first component transforming as a left-handed spinor and the second as a right-handed spinor, while qV is a vector quaternion that gives the 4-momentum of the plane wave. The quaternion-valued plane wave is:
ψ(x) = (qL, qR) exp(–i qV · x)
We can also develop a description of the angular momentum of a spin-1 particle, such as a Riemannian photon, that uses the quaternions. The vector representation of SU(2)×SU(2), the double cover of SO(4), is really just a representation on quaternions, in which the group SU(2) corresponds to the unit quaternions, and a pair of unit quaternions (g, h) in SU(2)×SU(2) acts on the quaternions themselves via:
(g, h) q → gqh–1 = gqh*
If we identify the quaternions, H, with four-dimensional Euclidean space, R4, then this representation corresponds to multiplying vectors in R4 by elements of SO(4): real, orthogonal 4×4 matrices with a determinant 1. This is fine when we’re doing classical physics and simply want to talk about rotating real four-vectors, but the angular momentum of a particle with spin 1 is a vector in a complex Hilbert space. How can we connect the two?
The solution is to “complexify” the quaternions. Just as we write a general complex number as a + b i where a and b are real numbers, we write a general complexified quaternion as q + s i, where q and s are quaternions. The i here should not be taken to be any of the square roots of minus 1 within the quaternions themselves, or to be the same as the right-multiplication by Hz that we use on the spinor quaternions. (Only when we multiply a complexified vector quaternion by a spinor to get another spinor do we convert factors of i to right-multiplication by Hz.) Within the complexified quaternions themselves, i is just a symbol that commutes with everything and satisfies i2=–1. So if we multiply two complexified quaternions, we have:
(q + s i)(p + r i) = (qp – sr) + (sp + qr) i
In working with the complexified quaternions, we’ll use the following conventions: “ReH” means the real part of a quaternion, as distinct from the real part of a complex number, which we’ll write “ReC”. We’ll use “*” to denote the conjugate of a quaternion, and “conj” to denote ordinary complex conjugation. So for example, in the equation below we take the opposite of all the quaternionic components orthogonal to Ht; we don’t reverse the sign of the coefficient of i.
((Ht + Hx) + (Ht + Hy) i)* = (Ht – Hx) + (Ht – Hy) i
There’s a real inner product, or dot product, defined on the quaternions:
q · s = ReH(q* s) = ½(q* s + s* q)
This is invariant under the action of SU(2)×SU(2); if we act with the pair of unit quaternions (g, h) we get:
q · s → (g q h–1) · (g s h–1)
= ½((g q h–1)* (g s h–1) + (g s h–1)* (g q h–1))
= ½(h q* g–1 g s h–1 + h s* g–1 g q h–1)
= ½(h q* s h–1 + h s* q h–1)
= ½(h (q* s + s* q) h–1)
= h ReH(q* s) h–1
= ReH(q* s)
= q · s
We extend this dot product to the complexified quaternions simply by requiring it to be complex-linear in each vector:
(q + s i) · (p + r i) = (q · p – s · r) + (s · p + q · r) i
We also need an inner product on the Hilbert space of complexified quaternions that is linear in the second argument and conjugate-linear (in the complex structure sense!) in the first argument:
< q + s i, p + r i >V = conj(q + s i) · (p + r i)
= (q – s i) · (p + r i)
= (q · p + s · r) + (q · r – s · p) i
We use a subscript of “V” on this inner product, standing for vector, to distinguish it from the inner product on the spinor quaternions:
< p, q >S = ReH(p* q) – ReH(p* q Hz) i
We’ve shown that the dot product is invariant under the action of SU(2)×SU(2), so our complex inner product < >V will be invariant too – or in other words, our representation of SU(2)×SU(2) is unitary, as it must be.
So far, we’ve taken a largely purist approach where we treat the quaternions as being fundamental mathematical objects, and this gives us formulas that are useful for many kinds of calculations. But sometimes it’s worth recalling that we can treat the ordinary quaternions as a subspace of the 2×2 complex matrices, spanned by real linear combinations of the four matrices Hμ – and in that context we can treat the complexified quaternions as arbitrary 2×2 complex matrices, which can be obtained as complex linear combinations of the Hμ.
Thinking of complexified vector quaternions as 2×2 complex-valued matrices, and spinor quaternions as lying in the smaller subspace spanned by the real linear combinations of the Hμ, the vector and spinor inner products can be written as:
< p, q >V = ½ tr(conj(pT) q)
< p, q >S = < p, q – i q Hz >V = ½ tr(conj(pT) (q – i q Hz))
When we treat the complexified quaternions as the Hilbert space for a Riemannian photon’s spin, we take the “pure” quaternions with no factor of i as states of linear polarisation, corresponding to the direction of the four-potential vector A in a classical Riemannian vector plane wave. In a reference frame in which the photon is at rest, the quaternions Hx, Hy and Hz are state vectors for the three linear polarisations of a plane wave, all of them orthogonal to its propagation vector (which in this case is Ht, since we’re in the rest frame).
The three vectors Hx, Hy and Hz can also be thought of as the states of a spin-1 particle whose component of spin in the x, y and z directions respectively is zero. This ties in precisely with the non-relativistic quantum mechanics of a spin-1 particle (one with mass, unlike photons in our universe), where choosing a basis of C3 consisting of states with a spin component of zero in each of three orthogonal directions allows the spin-1 representation of SU(2) on C3 to be identified with the vector representation of SO(3) on R3. In this basis, the spin-1 unitary matrices that are applied to C3 to represent rotations become real-valued – and in fact become exactly the same as the SO(3) matrices for the rotations.
What about the states where the particle has a spin component of plus or minus 1 along some axis? We can find these states by mimicking the relationship between circular polarisation and linear polarisation in classical waves. In a classical plane wave, circular polarisation around the z-axis, say, occurs when a wave with linear polarisation along the x-axis is combined with another with linear polarisation along the y-axis that is 90° out of phase with the first. For a complex exponential the 90° phase shift can be created by multiplication by i. So we expect the normalised photon states with one unit of spin along the z-axis to be given by (Hx ± i Hy)/√2. However, because of the same twist that leads us to use the opposite of the Pauli spin matrices for fermions, we need to choose the signs here carefully: the sum is the negative spin eigenstate and the difference is the positive spin eigenstate.
| Complexified vector quaternion states for a spin-1 particle | |
| Complexified vector quaternion | Angular momentum component |
| Hx | mx = 0 |
| Hy | my = 0 |
| Hz | mz = 0 |
| (Hy ± i Hz)/√2 | mx = –1, 1 |
| (Hz ± i Hx)/√2 | my = –1, 1 |
| (Hx ± i Hy)/√2 | mz = –1, 1 |
| Ht | mx = my = mz = 0 |
From these states we can construct operators for the spin along each axis, by projecting onto the spin eigenstates and multiplying by the spin. For example:
Jz(v) = – [(Hx + i Hy)/√2] < (Hx + i Hy)/√2, v >V + [(Hx – i Hy)/√2] < (Hx – i Hy)/√2, v >V
= i (Hx < Hy, v >V – Hy < Hx, v >V)
= i (Hx (Hy · v) – Hy (Hx · v))
In going from the second-last line to the last, we’ve used the fact that the complex inner product becomes identical to the dot product when the first argument has no imaginary part.
We will write this as:
Jz = i (Hx ⊗ Hy – Hy ⊗ Hx)
with the convention that this acts on any complexified quaternion via the dot product with the right-hand term in each tensor product. Similarly, we have:
Jx = i (Hy ⊗ Hz – Hz ⊗ Hy)
Jy = i (Hz ⊗ Hx – Hx ⊗ Hz)
Apart from a factor of –i, if we treated these operators as matrices acting on R3 they would just be the so(3) elements generating rotations around their respective axes.
Of course the full Hilbert space we’re working in has four complex dimensions, not three. Whatever we choose as a basis for the three-dimensional subspace of spins available to a photon at rest, we need a fourth vector such as Ht to allow us to deal with the general case of photons in motion.
In order to describe the interactions between Riemannian photons and electrons, we need to be able to construct intertwiners between the representations of SU(2)×SU(2) that apply to these particles, both in the case of individual particles and when we have, say, a system comprised of a photon and an electron. When we’re dealing with such a composite system, the representation that applies to the particles’ joint quantum state is the tensor product of the representations that apply individually:
ρphoton and electron(g, h) φphoton ⊗ ψelectron = (ρphoton(g, h) φphoton) ⊗ (ρelectron(g, h) ψelectron)
The representations that apply to individual particles are irreducible, but these tensor product representations are not. Rather, they are equivalent to a direct sum of two or more irreducible representations. What this means is that there will be subspaces within the tensor product vector space that are invariant under the representation – no vector within these subspaces is taken out of them by the representation – and each subspace will be equivalent to some irreducible representation. The simplest example of this is the tensor product of two spin-½ representations of SU(2), which contains one subspace equivalent to the spin-0 representation of SU(2) and another equivalent to the spin-1 representation of SU(2). We can write this in a kind of shorthand as ½ ⊗ ½ = 0 ⊕ 1. We actually defined the spin-j representation as sitting inside a tensor product of 2j copies of the spin-½ representation, so that discussion is a good place to see this idea worked out in more detail.
More generally, if we tensor the spin-j representation of SU(2) with the spin-k representation, the resulting space splits up into subspaces with spins ranging from |j–k| to j+k in steps of 1:
j ⊗ k = |j–k| ⊕ |j–k|+1 ⊕ ... ⊕ j+k
When it comes to representations of SU(2)×SU(2), which are described by a pair of spins, we have:
(j1, j2) ⊗ (k1, k2) = (|j1–k1|, |j2–k2|) ⊕ (|j1–k1|+1, |j2–k2|) ⊕ ... ⊕ (j1+k1, j2+k2)
with the left-hand spins taking on every value, in integer steps, between |j1–k1| and j1+k1, and the right-hand spins independently taking on every value, in integer steps, between |j2–k2| and j2+k2.
Now, our goal is to describe processes such as an electron absorbing a photon, in which we start with a composite system consisting of the electron and the photon, and end up with only the electron. We can build up a description of this from more elementary pieces, in which rather than starting with a photon and a complete Dirac spinor, we start with a photon and either a left- or right-handed spinor. In these cases, quaternion multiplication gives us an extremely simple intertwiner between the representation for the initial composite system and that which applies to a spinor of the opposite chirality. In other words, we can describe a left-handed spinor absorbing a photon and becoming a right-handed spinor, or a right-handed spinor absorbing a photon and becoming a left-handed spinor.
Before proceeding, we’ll tabulate the interpretation of the basis quaternions as spinors.
| Quaternion states for a spin-½ particle | ||
| Complex structure is right-multiplication by Hz | ||
| Basis quaternion | Interpreted as a spinor state | Angular momentum component |
| Ht | UP | mz = ½ |
| Hz | i UP | mz = ½ |
| Hy | –DOWN | mz = –½ |
| Hx | –i DOWN | mz = –½ |
The overall choice of phase is arbitrary, but this assignment gives us a consistent scheme for interpreting all the quaternions as spin states of a spin-½ particle. Recall that the whole two-real-dimensional plane spanned by Ht and Hz is to be thought of as a single complex plane, and the same is true for the plane spanned by Hx and Hy.
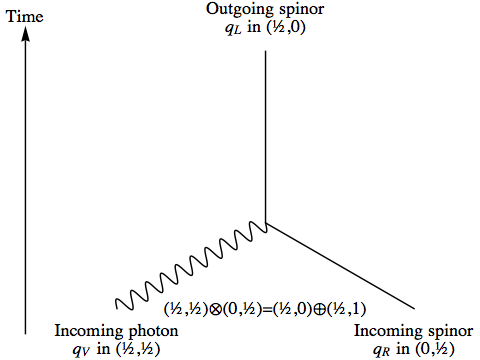
Let’s start by supposing that a particle described by a right-handed spinor qR absorbs a photon qV and turns into a left-handed spinor, qL. For now, what we’re exploring is just the spin, so we’re not concerned at all with the energy and momentum of these particles. Under a rotation described by the pair of unit quaternions (g, h), each of these quaternions transforms differently:
qR → h qR
qV → g qR h–1
qL → g qL
However, we can see that the product, qV qR, transforms just like a left-handed spinor:
(qV qR) → (g qV h–1) (h qR)
= g (qV qR)
If this business of a right-handed spinor becoming left-handed seems a bit mysterious when it’s done with quaternions, we can see why this is required by looking at the representations of SU(2)×SU(2):
(½, ½) ⊗ (0,½) = (½, 0) ⊕ (½, 1)
The (½, ½) representation is the photon, the (0,½) representation is the right-handed spinor, and the (½, 0) representation is a subspace of the tensor product that transforms just like a left-handed spinor. The remaining subspace in the tensor product, which transforms according to a (½, 1) representation, involves a total spin of 3/2; we’re assuming that no elementary particle with that spin exists, so this representation is only realised by the right-handed spinor and the photon remaining as separate entities.
As a candidate for an intertwiner from the space describing systems of photons and right-handed spinors to the space describing left-handed spinors, we will propose:
T1(qV ⊗ qR) = qV qR / 2
The reason for the particular normalisation factor of ½ will be explained shortly. Let’s see what this intertwiner gives us for various initial composite systems.
T1(Photon with mz = 0, UP spinor)
= T1(Hz ⊗ Ht)
= Hz Ht / 2
= Hz / 2
= [i/2] UP
A spin-UP right-handed spinor can absorb a photon with no spin along the z-axis to produce a spin-UP left-handed spinor, with an amplitude for this process of i/2.
T1(Photon with mz = 0, DOWN spinor)
= T1(Hz ⊗ (–Hy))
= –Hz Hy / 2
= Hx / 2
= [–i/2] DOWN
A spin-DOWN right-handed spinor can absorb a photon with no spin along the z-axis to produce a spin-DOWN left-handed spinor, with an amplitude of –i/2.
T1(Photon with mz = –1, UP spinor)
= T1((Hx + i Hy)/√2 ⊗ Ht)
= (Hx + i Hy) Ht / (2 √2)
= (Hx + i Hy) / (2 √2)
= (Hx + Hy Hz) / (2 √2)
= (2 Hx) / (2 √2)
= [–i/√2] DOWN
In going from the fourth line to the fifth, we’ve made use of the complex structure of the spinor quaternions, converting the factor of i that started out as an independent number in the complexified vector quaternions into right-multiplication by Hz. The conclusion: a spin-UP right-handed spinor can absorb a photon with a spin of –1 along the z-axis to produce a spin-DOWN left-handed spinor, with an amplitude of –i/√2.
T1(Photon with mz = –1, DOWN spinor)
= T1((Hx + i Hy)/√2 ⊗ (–Hy))
= –(Hx + i Hy) Hy / (2 √2)
= –(Hz – i Ht) / (2 √2)
= –(Hz – Hz) / (2 √2)
= 0
A spin-DOWN right-handed spinor and a photon with a spin of –1 along the z-axis have ZERO amplitude to produce any left-handed spinor.
T1(Photon with mz = 1, UP spinor)
= T1((Hx – i Hy)/√2 ⊗ Ht)
= (Hx – i Hy) Ht / (2 √2)
= (Hx – i Hy) / (2 √2)
= (Hx – Hy Hz) / (2 √2)
= (Hx – Hx) / (2 √2)
= 0
A spin-UP right-handed spinor and a photon with a spin of 1 along the z-axis have ZERO amplitude to produce any left-handed spinor.
T1(Photon with mz = 1, DOWN spinor)
= T1((Hx – i Hy)/√2 ⊗ (–Hy)
= –(Hx – i Hy) Hy / (2 √2)
= –(Hz + i Ht) / (2 √2)
= –(Hz + Ht Hz) / (2 √2)
= –(2 Hz) / (2 √2)
= [–i/√2] UP
A spin-DOWN right-handed spinor can absorb a photon with a spin of 1 along the z-axis to produce a spin-UP left-handed spinor, with an amplitude of –i/√2.
Finally, we note that:
T1(Ht ⊗ UP) = ½ UP
T1(Ht ⊗ DOWN) = ½ DOWN
Ht is not a possible state for the spin of a photon at rest, but it certainly has a z-component of spin of 0, i.e. Jz(Ht) = 0, so it makes sense that it can leave the direction of spin of our spinor unchanged.
As we would hope, we get an amplitude of zero whenever there is no left-handed spinor we can produce while conserving the z-component of spin. For the other cases, though, the probabilities – the squared norms of the amplitudes – aren’t 1. For example, we don’t have a probability of 1 for a spin-UP spinor and a photon with zero spin along the z-axis to yield another spin-UP spinor. Why not? Because this state is not an eigenstate for total spin. It is an eigenstate for the z-component of the spin, mz=½, but there’s a non-zero amplitude for the total spin j of the composite system to be 3/2 rather than ½, as we can see by recalling our decomposition of the tensor product space:
(½, ½) ⊗ (0,½) = (½, 0) ⊕ (½, 1).
The normalisation we’ve chosen for the intertwiner makes the squared norms of the amplitudes for all the different ways of creating a spin-UP spinor add up to 1:
|T1(Photon with mz = 0, UP spinor)|2 + |T1(Photon with mz = 1, DOWN spinor)|2 + |T1(Ht ⊗ UP)|2
= |i/2|2 + |–i/√2|2 + |½|2
= ¼ + ½ + ¼
= 1
The same holds for the different ways of creating spin DOWN. This lets us think of each of the amplitudes we get from the intertwiner as the inner product between one of our initial states and one of two normalised vectors sitting in the composite system’s Hilbert space, in the subspace that transforms under the (½, 0) representation. For both these vectors the total spin j is ½, and the z-component mz is ½ or –½ respectively. So the intertwiner, normalised this way, is giving us amplitudes for measuring j and mz and finding them to have these particular values.
We can do something similar for a left-handed spinor absorbing a photon and turning into a right-handed spinor. We define:
T2(qV ⊗ qL) = –qV* qL / 2
The minus sign will turn out to be a convenient choice later. Remember that the * operation here conjugates quaternions, but has no effect on the number i in our complexified quaternions. The result transforms as a right-handed spinor under the rotation (g, h):
(qV* qL) → (g qV h–1)* (g qL)
= (h qV g–1) (g qL)
= h (qV qL)
where g–1=g* and h–1=h* because these are unit quaternions.
We can combine the two intertwiners for left- and right-handed spinors to give an intertwiner for a Riemannian Dirac particle absorbing a photon:
T3(qV ⊗ (qL, qR)) = (qV qR, –qV* qL) / 2
Since the Dirac particle has both left- and right-handed components, the same representation applies before and after it absorbs the photon. Keep in mind, though, that this still has nothing to do with energy and momentum conservation; we’re only looking at spin.
Before we go on to look at other interactions involving photons and electrons, we’ll describe some intertwiners that connect the representations for photons and electrons to the trivial representation of SO(4). The trivial representation describes the way a particle of spin 0 transforms: it’s completely unchanged by a change of coordinates. The Hilbert space associated with its spin is one-complex-dimensional, i.e. it’s just the complex numbers C. So an intertwiner that describes two photons combining to yield a particle of spin 0 will be a function from the tensor product of two copies of the complexified quaternions to the complex numbers, such that the value of the function is unchanged when the same rotation is applied to the two photons.
Such a function is very easy to find: it’s just the dot product! With a suitable normalisation factor, we define:
T4(qV1 ⊗ qV2) = qV1 · qV2 / 2
It’s more or less a definition of what a rotation is that the value of the dot product will be unchanged when the same rotation is applied to qV1 and qV2. And it’s easy to check that a state where two photons have a spin component of zero along the same axis, such as Hz ⊗ Hz, yields a non-zero result, as does a state where one photon has the opposite spin to the other, while a state where two photons have the same non-zero spin will yield zero.
It’s not much harder to describe an intertwiner that goes the other way, taking a particle with spin 0 and giving a state in the Hilbert space of two-photon systems that, like the spin-0 particle, is invariant under rotations.
T5(z) = (z/2) (Hx ⊗ Hx + Hy ⊗ Hy + Hz ⊗ Hz + Ht ⊗ Ht)
We choose the normalisation so that when z is a unit complex number, T5(z) is a unit vector. The easiest way to see why T5(z) is invariant under rotations is to think of it as being like the metric tensor in flat Euclidean space: a matrix with 1 for every diagonal entry. Just as the metric is unchanged by rotations, so is this state. (Strictly speaking, if we’re think of the quaternions as vectors this tensor state is like the metric on the dual space of linear functions of vectors, but that’s unchanged by rotations just like the metric on the vector space.)
Our previous interwiner, T4, can be thought of as giving the inner product between the normalised invariant vector T5(1) and its argument:
T4(qV1 ⊗ qV2) = < T5(1), qV1 ⊗ qV2 >V⊗V
We get an inner product on the tensor product space simply by multiplying inner products between the individual terms in each tensor:
< a ⊗ b, c ⊗ d >V⊗V = < a, c >V < b, d >V
If we compose these two intertwiners, we get:
T4(T5(z)) = ¼ z (Hx · Hx + Hy · Hy + Hz · Hz + Ht · Ht) = z
What about an invariant state for two spinors? We define:
T6(z) = (z/√2) (UP ⊗ DOWN – DOWN ⊗ UP)
= (z/√2) (Hy ⊗ Ht – Ht ⊗ Hy)
This state can be interpreted either as two left-handed spinors or two right-handed spinors; in either case it will be invariant under SO(4). The effect of a rotation is to multiply every quaternion here on the left by the same unit quaternion; we’ll leave a general proof of invariance as an exercise, and only work through one specific example, where the quaternion from the rotation is Hx.
Hy ⊗ Ht – Ht ⊗ Hy → (Hx Hy) ⊗ (Hx Ht) – (Hx Ht) ⊗ (Hx Hy)
= (Hz) ⊗ (Hx) – (Hx) ⊗ (Hz)
= – (Hz Hz) ⊗ (Hx Hz) + (Hx Hz) ⊗ (Hz Hz) [Multiplying first tensor factor by –i and second by i]
= – Ht ⊗ Hy + Hy ⊗ Ht
Finally, we need an intertwiner that takes a pair of spinors of the same chirality (both left-handed or both right-handed) and gives a complex number that’s invariant when we rotate the spinors. An obvious candidate is the inner product of the two-spinor state with our rotationally-invariant state, T6(1).
T7(qL1 ⊗ qL2) = < T6(1), qL1 ⊗ qL2 >S⊗S
= (1/√2) [ < Hy, qL1 >S < Ht, qL2 >S – < Ht, qL1 >S < Hy, qL2 >S ]
Though the simplification to the form below is laborious when performed with step-by-step transformations, it’s easy to verify. Both expressions are complex-linear in qL1 and qL2, and both give identical results when evaluated on four basis vectors: Ht ⊗ Ht, Hy ⊗ Hy, Hy ⊗ Ht and Ht ⊗ Hy.
T7(qL1 ⊗ qL2) = (1/√2) < qL2 Hy, qL1 >S
= (1/√2) [ReH(qL1* qL2 Hy) + i ReH(qL1* qL2 Hx)]
If we compose these two intertwiners between spin 0 and spin ½ ⊗ spin ½, we get:
T7(T6(z)) = ½ z [ ReH(Hy* Ht Hy) + i ReH(Hy* Ht Hx) – ReH(Ht* Hy Hy) – i ReH(Ht* Hy Hx) ]
= ½ z [ 1 + 0 – (–1) – 0 ]
= z
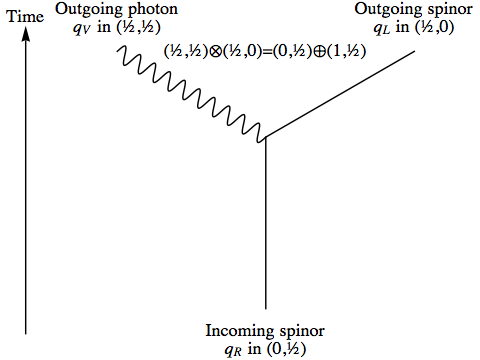
If we want to describe a process where a spinor emits a photon, we can make use of the following trick: we pretend that our spinor is accompanied by a spin-0 particle, which decays into two photons. The spinor absorbs one photon, while the other goes on its way. Since we’re only concerned with spin representations, not energy and momentum, the initial state of a spinor and a spin-0 particle transforms just like a spinor alone, and we end up with a photon and a spinor of the opposite chirality, just as if it were the spinor that emitted the photon. We don’t have to take any of this literally; the point is that it gives us a map between the spaces we need with exactly the right transformation properties.
So, we define:
T8(qR) = T '1(T5(1) ⊗ qR)
T5(1) gives us a pair of photons that we tensor with our right-handed spinor, then we use a new intertwiner T '1 to describe the absorption of either of those photons, leaving the other untouched. We obtain T '1 by extending the definition of T1 to allow for an extra photon:
T '1(qV1 ⊗ qV2 ⊗ qR) = ½ (qV1 ⊗ (qV2 qR) + qV2 ⊗ (qV1 qR))
Spelling this out, we get:
T8(qR) = ½ T '1((Hx ⊗ Hx + Hy ⊗ Hy + Hz ⊗ Hz + Ht ⊗ Ht) ⊗ qR)
= ½ [Hx ⊗ (Hx qR) + Hy ⊗ (Hy qR) + Hz ⊗ (Hz qR) + Ht ⊗ (Ht qR)]
= ½ Σμ [Hμ ⊗ (Hμ qR)]
The first space in the final tensor product here is the photon that’s emitted, while the second space is the now-left-handed spinor.
For example, suppose our original spinor has spin UP, qR = Ht. Then the result is:
T8(UP) = ½ [Hx ⊗ Hx + Hy ⊗ Hy + Hz ⊗ Hz + Ht ⊗ Ht]
= ½ [–i Hx ⊗ DOWN – Hy ⊗ DOWN + i Hz ⊗ UP + Ht ⊗ UP]
= ½ [–i (Hx – i Hy) ⊗ DOWN + i (Hz – i Ht) ⊗ UP]
The first term here, (Hx – i Hy) ⊗ DOWN, describes a photon with mz=1 and a spinor with spin DOWN (i.e. mz=–½), so their total z-component of spin is ½, the same as the original spinor. In the second term, (Hz – i Ht) ⊗ UP, the photon part is an eigenstate of Jz with an eigenvalue of zero, so again we have conservation of the z-component of spin, although this photon polarisation is only possible for a particle in motion.
To describe a Dirac spinor emitting a photon, we combine versions of the construction that use T '1 and a similarly defined T '2:
T9(qL, qR) = ½ (T '1((Hx ⊗ Hx + Hy ⊗ Hy + Hz ⊗ Hz + Ht ⊗ Ht) ⊗ qR), T '2((Hx ⊗ Hx + Hy ⊗ Hy + Hz ⊗ Hz + Ht ⊗ Ht) ⊗ qL))
= ½ Σμ [Hμ ⊗ (Hμ qR, –Hμ* qL)]
What if we have a Dirac spinor emit a photon with T9, and then feed the result into T3, so that the spinor re-absorbs the photon it emitted?
T3(T9(qL, qR)) = ¼ Σμ (–Hμ Hμ* qL, –Hμ* Hμ qR) = –(qL, qR)
So we get back the original Dirac spinor, multiplied by minus one.
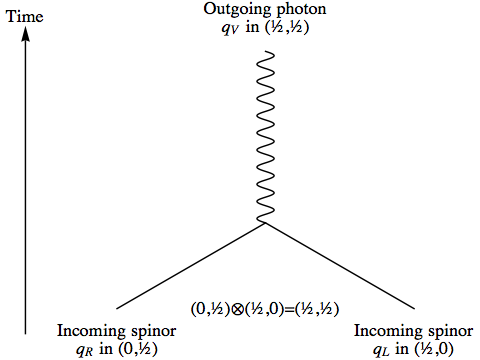
When an electron and a positron annihilate, the only way that energy and momentum can be conserved is for two photons to be created. In fact, the same criterion applies to a free electron absorbing or emitting a photon: the electron has to scatter an incoming photon, it can’t absorb or emit a single photon.
But in this section we’re only concerned with spin, not energy and momentum, so we’ll go ahead and construct an intertwiner for an electron and a positron coming together and creating a single photon. This is actually a useful thing to have, because this kind of interaction, where just three elementary particles are involved, can be seen as one step within a larger process where energy and momentum are conserved: one vertex in a larger Feynman diagram.
To combine two spinors to make a vector, one spinor must be left-handed and the other right-handed. We can use two of the intertwiners we’ve constructed previously to meet our needs here: T8 to turn a right-handed spinor into a left-handed spinor and a photon, and then T7 to combine the new left-handed spinor with the original left-handed spinor to get a spin-0 particle – a complex number we can simply multiply into our result.
Recall that:
T8(qR) = ½ Σμ [Hμ ⊗ (Hμ qR)]
T7(qL1 ⊗ qL2) = < (Hy ⊗ Ht – Ht ⊗ Hy)/√2, qL1 ⊗ qL2 >S⊗S
Instead of simply combining these intertwiners, though, we’ll create a version that treats the left- and right-handed spinors equally, having the initially left-handed spinor play a role in emitting the photon as well.
T10(qL ⊗ qR) = 1/(2√2) Σμ < Hy ⊗ Ht – Ht ⊗ Hy, qL ⊗ (Hμ qR) – qR ⊗ (Hμ* qL) >S⊗S Hμ
= 1/(2√2) Σμ [< Hy, qL >S < Ht, Hμ qR >S – < Ht, qL >S < Hy, Hμ qR >S
– < Hy, qR >S < Ht, Hμ* qL >S + < Ht, qR >S < Hy, Hμ* qL >S] Hμ
Simplifying the expression above is a lot of work, but we can actually go a long way to anticipating the answer from some basic principles. The only combination of left- and right-handed spinors that will transform as a complexified vector quaternion would be:
qL (a + i b) qR*
In order for this expression to be complex-linear, if we right-multiply either qL or qR with Hz the result must be the same as multiplying through by i, and so:
Hz b = –b Hz = a
Hz a = –a Hz = –b
Setting b = Hx gives a = Hy in the first of these equations, and these values satisfy the second equation as well. Any real multiple of the same choices will work, and it’s not hard to verify that we can match our original definition precisely if we set:
T10(qL ⊗ qR) = –(i/√2) qL (Hx – i Hy) qR*
For example:
T10(UP ⊗ UP) = T10(Ht ⊗ Ht) = –(i/√2) (Hx – i Hy)
The result is –i times our normalised photon state with mz=1. We also have:
T10(DOWN ⊗ DOWN) = T10((–Hy) ⊗ (–Hy))
= (i/√2) Hy (Hx – i Hy) Hy
= (i/√2) (Hx + i Hy)
So the result is just i times our normalised photon state with mz=–1. For other combinations of spinors we get:
T10(UP ⊗ DOWN) = T10(Ht ⊗ (–Hy))
= –(i/√2) (Hx – i Hy) Hy
= –(i/√2) (Hz + i Ht)
T10(DOWN ⊗ UP) = T10((–Hy) ⊗ Ht)
= (i/√2) Hy (Hx – i Hy)
= –(i/√2) (Hz – i Ht)
In both cases the result is a normalised eigenstate with mz=0. At first glance it might seem like a mistake or a problem that these results give us:
T10((UP ⊗ DOWN – DOWN ⊗ UP)/√2) = Ht
since that initial state looks like it ought to be an eigenstate with total spin 0, not 1! But the fact that one spinor is left-handed and the other right-handed makes all the difference here; the tensor product of the chiral representations is (½,0)⊗(0,½)=(½,½), i.e. the entire space has a total spin of 1.
T10 is an intertwiner for two single spinors. For two Dirac particles, we have:
T11((qL1, qR1) ⊗ (qL2, qR2)) = –(i/√2) (qL1 (Hx – i Hy) qR2* + qL2 (Hx – i Hy) qR1*)
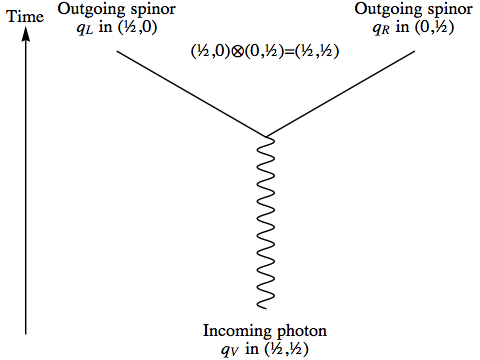
The reverse of the process we discussed in the last section involves a photon turning into two spinors, one left-handed and one right-handed. As with our other examples, this is not something a free photon can do while conserving energy and momentum, but we’re still interested in understanding the relationship between the spins.
The trick we’ll use to get this intertwiner is to imagine a spin-0 particle decaying into a pair of right-handed spinors, one of which simply goes on its way, while the other one absorbs our photon and turns into a left-handed spinor. We combine this with a version where we get a pair of left-handed spinors instead, one of which goes on its way, while the other absorbs the photon and becomes right-handed. As with our other constructions, this isn’t meant to be taken literally; we’re simply exploiting the fact that tensoring our initial state with a spin-0 representation has no effect on the way it transforms.
The pairs of spinors (whether both left-handed or both right-handed) that come from our fictitious spin-0 particle are given by the normalised state:
T6(1) = (1/√2) (UP ⊗ DOWN – DOWN ⊗ UP)
= (1/√2) (Hy ⊗ Ht – Ht ⊗ Hy)
We absorb the photon in processes modelled on our intertwiners T1 and T2, leaving a state with one left-handed spinor and one right-handed spinor:
T12(qV) = (1/(2√2)) ((qV Hy) ⊗ Ht – (qV Ht) ⊗ Hy + Hy ⊗ (qV* Ht) – Ht ⊗ (qV* Hy) )
Some examples:
T12(Photon with mz=1) = T12((Hx – i Hy)/√2)
= ¼ [((Hx – i Hy) Hy) ⊗ Ht – ((Hx – i Hy) Ht) ⊗ Hy – Hy ⊗ ((Hx – i Hy) Ht) + Ht ⊗ ((Hx – i Hy) Hy) ]
= ¼ [(Hz + Hz) ⊗ Ht – (Hx – Hx) ⊗ Hy – Hy ⊗ (Hx – Hx) + Ht ⊗ (Hz + Hz)]
= ½ [Hz ⊗ Ht + Ht ⊗ Hz]
= i UP ⊗ UP
T12(Photon with mz=–1) = T12((Hx + i Hy)/√2)
= ¼ [((Hx + i Hy) Hy) ⊗ Ht – ((Hx + i Hy) Ht) ⊗ Hy – Hy ⊗ ((Hx + i Hy) Ht) + Ht ⊗ ((Hx + i Hy) Hy) ]
= ¼ [(Hz – Hz) ⊗ Ht – (Hx + Hx) ⊗ Hy – Hy ⊗ (Hx + Hx) + Ht ⊗ (Hz – Hz)]
= –½ [Hx ⊗ Hy + Hy ⊗ Hx]
= –i DOWN ⊗ DOWN
T12(Photon with mz=0) = T12(Hz)
= (1/(2√2)) [(Hz Hy) ⊗ Ht – (Hz Ht) ⊗ Hy – Hy ⊗ (Hz Ht) + Ht ⊗ (Hz Hy) ]
= –(1/(2√2)) [Hx ⊗ Ht + Hz ⊗ Hy + Hy ⊗ Hz + Ht ⊗ Hx]
= –(1/(2√2)) [(–i DOWN) ⊗ UP + (i UP) ⊗ (–DOWN) + (–DOWN) ⊗ (i UP) + UP ⊗ (–i DOWN)]
= (i/√2) (DOWN ⊗ UP + UP ⊗ DOWN)
T12(Ht)
= (1/√2) (Hy ⊗ Ht – Ht ⊗ Hy)
= (1/√2) (UP ⊗ DOWN – DOWN ⊗ UP)
If we apply the intertwiner T10 to any of these specific results, we get back the original photon state. Since they constitute a set of basis vectors, this must be true for any state at all:
T10(T12(qV)) = qV
We have constructed intertwiners that we can use to describe:
We should stress, once again, that we’re only looking at the spins of these particles; conserving energy and momentum is a separate issue.
Now, from a completely objective point of view in which we refuse to favour any particular observer, all of these processes are examples of the same thing: an interaction between two spinors and a photon. By rotating our frame of reference, we can turn any one of these processes into any other.
In the case where two observers have the same account of which particles are present before and after the interaction, the rotational invariance of the result can be seen very easily. For example, suppose one observer, Carla, says an electron absorbed a photon, and attributed the state qV to the photon and the Dirac spinor (qL1, qR1) to the electron initially. If she is interested in the amplitude for the electron to end up with the Dirac spinor (qL2, qR2), she will use the intertwiner T3 to compute this as:
A = < (qL2, qR2), T3(qV ⊗ (qL1, qR1)) >D
= ½ < (qL2, qR2), (qV qR1, qV* qL1) >D
= ½ [ < qL2, qV qR1 >S + < qR2, qV* qL1 >S ]
Here we have defined an inner product on Dirac spinors, < >D, as the sum of the spinor inner products < >S between the left and right hand spinors.
If another observer, Patrizia, agrees that a photon absorbed an electron, but is using a set of coordinates rotated with respect to Carla’s by a pair of unit quaternions (g, h), she will attribute different spin states to the particles:
q'V = g qV h–1
(q'L1, q'R1) = (g qL1, h qR1)
(q'L2, q'R2) = (g qL2, h qR2)
Using the same intertwiner, but applying it to her own versions of the spin states, Patrizia will predict an amplitude that’s exactly the same as Carla’s:
A' = ½ [ < q'L2, q'V q'R1 >S + < q'R2, q'V* q'L1 >S ]
= ½ [ < g qL2, g qV h–1 h qR1 >S + < h qR2, h qV* g–1 g qL1 >S ]
= ½ [ < g qL2, g qV qR1 >S + < h qR2, h qV* qL1 >S ]
= ½ [ < qL2, qV qR1 >S + < qR2, qV* qL1 >S ]
= A
To go from the third-last line to the second-last, we use the fact that the spinor inner product is invariant when both arguments are multiplied on the left by the same unit quaternion, which we established previously.
The situation becomes trickier, though, when different observers disagree over which particles were present before the interaction and which are present after. To compare the measurements and predictions of such observers, not only do we need to switch from one of our four intertwiners to another, we need to do more than transform the particles’ spin states with the usual representations.
Why? Classically, spin depends on the direction that an object is rotating as you watch it move forwards in time. Just as there is no absolute energy-momentum vector, there is no absolute spin vector (or tensor); an object spinning counterclockwise around the z-axis as seen from above, by one observer, will be seen to be spinning clockwise by an observer with the opposite arrow of time.
However, we can talk objectively about the direction in which an object is spinning as it approaches a particular interaction. This will agree with the direction of spin for an observer who thinks of the object as being present before the interaction, but will be the opposite to the direction of spin for an observer who thinks of it as being present after the interaction. If we agree to express all spins in these terms, then (rather like the observer-independent approach to conservation of energy-momentum), we can see that angular momentum is conserved at every interaction.
Quantum mechanically, we can reverse the spins of our quaternionic spinors with the revS function we described previously:
revS(q) = q Hy
For the complexified vector quaternions we use for photon states, to reverse the spin we simply conjugate them in the complex-structure sense:
revV(p + q i) = con(p + q i) = p – q i
Once we’ve spin-reversed any of the states that we originally measured leaving the interaction rather than approaching it, we should find the tensor product of all three states to have a total spin of 0. We can quantify this with an intertwiner from the tensor product to spin 0, which we can construct by imagining the two spinors annihilating, and then taking the dot product between the resulting photon and the original:
Tvert(qV ⊗ qL ⊗ qR) = T4(qV ⊗ T10(qL ⊗ qR)) = –i/(2√2) qV · (qL (Hx – i Hy) qR*)
The intertwiner Tvert as we’ve constructed it is normalised in the sense that the sum, over any orthonormal basis of the tensor product space, of the squared magnitudes of the results is 1. These results can be thought of as inner products between a single normalised vector sitting in the tensor product space, an eigenstate of total spin with an eigenvalue of j=0, and whatever triple-particle state we feed to the intertwiner. However, we get some extra factors when we compare Tvert with our other intertwiners:
< qL, T1(qV ⊗ qR) >S = (√2) Tvert(qV ⊗ revS(qL) ⊗ qR) [Right-handed spinor absorbs photon to become left-handed]
< qR, T2(qV ⊗ qL) >S = (√2) Tvert(qV ⊗ qL ⊗ revS(qR)) [Left-handed spinor absorbs photon to become right-handed]
< qV ⊗ qL, T8(qR) >V⊗S = (√2) Tvert(revV(qV) ⊗ revS(qL) ⊗ qR) [Right-handed spinor emits photon and becomes left-handed]
< qV ⊗ qR, T8L(qL) >V⊗S = (√2) Tvert(revV(qV) ⊗ qL ⊗ revS(qR)) [Left-handed spinor emits photon and becomes right-handed]
< qV, T10(qL ⊗ qR) >V = 2 Tvert(revV(qV) ⊗ qL ⊗ qR) [Left- and right-handed spinors annihilate to create photon]
< qL ⊗ qR, T12(qV) >S⊗S = 2 Tvert(qV ⊗ revS(qL) ⊗ revS(qR)) [Photon turns into pair of left- and right-handed spinors]
[We didn’t bother to explicitly construct what we’ve called T8L here, a version of T8 that starts with a left-handed spinor, but the precise definition can be seen in the right-handed component of T9 for a full Dirac spinor, at the end of the section on electrons emitting photons.]
The factors of √2 and 2 appear because we normalised these various intertwiners according to which particle(s) are present initially. For example, we normalised T1 and T2 to give us the amplitude for the initial state to have a total spin of ½ and for the final state to be a particular spinor. Since the dimension of the subspace of the initial state space with a total spin of ½ is 2, if we sum over orthonormal bases for all the initial and final states we get a total for all the squared magnitudes of 2. But since Tvert gives amplitudes for the total spin to be 0, and only a 1-dimensional subspace of the initial state space meets that condition, the same kind of sum yields just 1. The factor of √2 is the square root of the ratio between the two.
To extract something completely observer-independent from this, suppose one observer has seen an interaction that definitely involved a left-handed spinor, a right-handed spinor, and a photon. They measured the states of all three particles, and then applied the spin-reversal function to any states that they saw as outgoing. Given the bases used for the three measurements, and the actual results for any two of the particles, we ought to be able to compute the relative probabilities for all the basis elements for the third particle, regardless of whether the original observer saw it as an incoming particle or an outgoing one.
We compute the relative probabilities as |Tvert(qV ⊗ qL ⊗ qR)|2, holding two of the states fixed at their known results while setting the third state to each element of the measurement basis in turn. We can then divide through by the sum of these values to get true probabilities. Because any overall factors cancel out in the normalisation, carrying out the same procedure with any of the six intertwiners listed above will give exactly the same probabilities as we get from Tvert. All the differences between the intertwiners apart from the overall normalisation are dealt with by the spin reversals.
Now that we’ve seen how to treat both vectors and spinors as quaternions, it’s not hard to convert other definitions and equations in Riemannian quantum electrodynamics into quaternionic form. As one simple example, we’ll look at the interaction term in the Riemannian QED Lagrangian:
Linter = –e Aμ ψ† γμ ψ
In quaternionic terms, and working in the Weyl basis, we have:
| ψ | = | (qL v0, qR v0) | |||||
| ψ† | = | (v0† qL*, v0† qR*) | |||||
| qV | = | Aμ Hμ | |||||
| γμ | = |
|
Here v0 is a unit vector in C2 that we use to map C2 to the quaternions; our usual choice is v0=(0,1) to be compatible with right-multiplication by Hz as the complex structure on the quaternions. We’re using † for the conjugate-transpose of complex vectors and matrices, and the * we use for quaternionic conjugation is really the same if we think of quaternions as 2×2 complex matrices.
So we have:
Linter = –e Aμ [ v0† qL* Hμ qR v0 + v0† qR* Hμ* qL v0 ]
= –e v0† [ qL* qV qR + qR* qV* qL ] v0
The quantity in brackets in the last line above is a pure real number as a quaternion, since it’s equal to its own quaternionic conjugate, so as a 2×2 matrix it’s just a multiple of the identity matrix. So we have:
Linter = –e (v0† v0) [ qL* qV qR + qR* qV* qL ]
= –e [ qL* qV qR + qR* qV* qL ]
It’s not hard to see that this is invariant under the usual transformations, given a pair of unit quaternions (g, h) in SU(2)×SU(2):
qV → g qV h–1
qL → g qL
qR → h qR
You might be wondering why we can’t use this function, Linter, as an intertwiner from photon-and-two-spinor states to spin 0. But the Lagrangian is a real number, and in this context qV is just an ordinary quaternion, not a complexified quaternion. The intertwiner Tvert that we already constructed is complex-linear in all three spin states. It is unique (up to an overall constant factor), and we can’t use the Lagrangian in its place.
As a check on our result, suppose that the left- and right-handed spinor quaternions actually satisfy the quaternionic Dirac equation for a plane wave with energy-momentum vector QV = kμ Hμ, which is:
QV qR – m qL = 0
We can write the interaction energy as the opposite of the Lagrangian, and then make the substitution qL = QV qR / m:
Hinter = –Linter
= e [ qL* qV qR + qR* qV* qL ]
= (e/m) [ qR* QV* qV qR + qR* qV* QV qR ]
= (e/m) qR* [ QV* qV + qV* QV ] qR
= (qR* qR) (e/m) [ QV* qV + qV* QV ]
= ½ (e/m) [ kμ Hμ* Aν Hν + Aν Hν* kμ Hμ ]
= ½ (e/m) kμ Aν [ Hμ* Hν + Hν* Hμ ]
= ½ (e/m) kμ Aν (2 δνμ)
= (e/m) kμ Aμ
where in going from the fourth line to the fifth we have used the fact that the expression in brackets is real (being the sum of QV* qV and its conjugate) and hence commutes with qR, and we then use qR* qR = |qR|2 = ½, which is the appropriate normalisation if we want ψ†ψ = 1.
This result is obviously invariant, and in a frame where the electron is at rest and k = m et it becomes:
Hinter = e At = –e V
where V is the potential energy. We expect a minus sign, since true, relativistic energy in the Riemannian universe is the opposite of potential energy.
We’ll begin our treatment of Riemannian quantum field theory by summarising some results from the non-relativistic quantum mechanics of a simple harmonic oscillator.
In fact, we’ll start with the classical mechanics of a simple harmonic oscillator. In classical physics, suppose we have a point particle of mass M, free to move in one dimension described by the coordinate x, and subject to a force F = –K x. This force, linear in the distance of the particle from the origin, corresponds to a potential energy of V = ½ K x2, an “energy valley” shaped like a parabola. The particle will oscillate back and forth in this valley with an angular frequency ω=√(K/M).
We can write the Hamiltonian for this system, the energy expressed in terms of the coordinate x and the associated momentum p, as:
HSHO = p2 / (2M) + ½ M ω2 x2
where we’ve written M ω2 in place of the “spring constant” K since the two quantities are identical, and ω will be of more interest to us than K.
If we put a dot above a quantity to represent its time derivative, Hamilton’s equations for this system are:
p• = –∂xHSHO
∂t p = –M ω2 x
x• = ∂pHSHO
∂t x = p / M
Combined, these give us:
∂t2x = –ω2 x
which has the general solution:
x(t) = A cos(ωt) + B sin(ωt)
If we describe the system instead with a Lagrangian, the kinetic energy minus the potential energy, expressed in terms of the coordinate x and its rate of change with time x•:
LSHO = ½ M (x•2 – ω2 x2)
then the Euler-Lagrange equation of motion gives us:
∂t (∂x•LSHO) = ∂xLSHO
∂t (M x•) = –M ω2 x
∂t2x = –ω2 x
which is of course the same equation as we obtained from the Hamiltonian.
When we analyse the same system in quantum mechanics, the numbers x and p that describe the particle’s position and momentum are replaced by “observables”: self-adjoint operators on a Hilbert space. One way to think of that Hilbert space is as a space of complex-valued wave functions ψ(x, t). The number x is replaced by the operator that consists of multiplying a wave function by x, while the number p is replaced by the differential operator –i ∂x. [We’re doing non-relativistic quantum mechanics here, so we don’t change the sign of the momentum operator the way we do with Riemannian relativistic QM.] Requiring the system to be described by a particular Hamiltonian then amounts to requiring that the wave function satisfies the Schrödinger equation:
i ∂t ψ(x, t) = H ψ(x, t)
= (p2 / (2M) + ½ M ω2 x2) ψ(x, t)
= –1 / (2M) ∂x2ψ(x, t) + ½ M ω2 x2 ψ(x, t)
But rather than going ahead and finding solutions to this differential equation, it’s more useful for our present purposes if we simply think of the Hilbert space for our quantised oscillator as being spanned by vectors with definite energies, or eigenvectors of the Hamiltonian, without worrying about the specifics of the corresponding wave functions. A more detailed treatment can be found in most introductory quantum mechanics textbooks[2].
First, we note that the commutator between the momentum and position operators is given by:
[x, p] = x p – p x = i
This is easily checked in the wave function representation of the operators, simply by noting that for any function f of x:
[x, p] f = [x, –i ∂x] f
= x (–i ∂x f ) – (–i ∂x (x f ))
= –i x ∂x f + i (f + x ∂x f )
= i f
From x and p we can construct two new operators, known as ladder operators:
a = i (p – i M ω x) / √(2 M ω)
a† = –i (p + i M ω x) / √(2 M ω)
Here a† is the Hermitian adjoint of a, and p and x are self-adjoint, so finding a† from a just amounts to changing the sign of every i in the first definition. From the commutator between x and p it’s not hard to show that:
[a, a†] = a a† – a† a = 1
From this, it’s easy to derive a number of results that we’ll make use of repeatedly:
a a† = a† a + 1
a† a a† = a† (a† a + 1)
a† a = a a† – 1
a† a a = (a a† – 1) a = a (a† a – 1)
We can express the Hamiltonian operator very simply in terms of the ladder operators:
HSHO = p2 / (2M) + ½ M ω2 x2
= ω (a†a + ½)
Now, suppose ψE is any eigenvector of the Hamiltonian, with:
HSHO ψE = E ψE
It then follows that:
HSHO (a† ψE)
= ω (a†a + ½) (a† ψE)
= a† ω (a†a + ½ + 1) ψE
= a† HSHO ψE + ω (a† ψE)
= (E + ω) (a† ψE)
So a† turns any eigenvector of the Hamiltonian into another eigenvector with an energy that is greater by ω. Similarly:
HSHO (a ψE)
= ω (a†a + ½) (a ψE)
= a ω (a†a + ½ – 1) ψE
= a HSHO ψE – ω (a ψE)
= (E – ω) (a ψE)
The operator a turns any eigenvector of the Hamiltonian into another eigenvector with an energy that is less by ω. But that process can’t go on forever, because the energy eigenvalues must be non-negative. So there must be some state ψ0 such that:
a ψ0 = 0
This is the “ground state” of the harmonic oscillator. And despite the subscript we’ve used, the energy of this ground state won’t be zero. Rather:
HSHO ψ0 = ω (a†a + ½) ψ0 = (ω/2) ψ0
So the energy of ψ0 is ω/2, and there’s an infinite succession of higher-energy eigenstates, with their energies equal to integer-plus-a-half multiples of ω:
ψn = (a†)n ψ0
HSHO ψn = (n + ½) ω ψn
When the oscillator is in an energy eigenstate — that is, when it possesses a definite energy – that energy can be thought of as the ground state energy, ω/2, plus a certain number n of additional “quanta”, each with energy ω. (If you’re used to thinking of quanta as having energy ℏ ω, remember that we’re using units where ℏ=1.) The operator a can be thought of as “annihilating” one quantum, because it turns an energy eigenstate into another with one less quantum. Similarly, the operator a† can be thought of as “creating” one quantum. So we will call a an annihilation operator and a† a creation operator. But although these terms are nice and evocative, they can’t be taken literally: these operators do not describe a physical process that takes place over time, they’re just an easy way to map states with definite numbers of quanta to other states with one less or one more.
Now, while everything we’ve done here describes a non-relativistic point particle undergoing simple harmonic motion, exactly the same analysis can be applied whenever the degrees of freedom of a system are governed by the same kind of Hamiltonian: a sum of terms proportional to the square of a coordinate and the square of the corresponding momentum. Since we’ll be making extensive use of these results, we summarise them in the following table.
| Simple Harmonic Oscillator | |||
| M is the mass of the particle ω is the frequency of oscillation We’re using units such that ℏ = 1 | |||
| HSHO | = | p2 / (2M) + ½ M ω2 x2 | (Hamiltonian) |
| LSHO | = | ½ M (x•2 – ω2 x2) | (Lagrangian) |
| ∂t2x | = | –ω2 x | (Equation of Motion) |
| a | = | i (p – i M ω x) / √(2 M ω) | (Annihilation Operator) |
| a† | = | –i (p + i M ω x) / √(2 M ω) | (Creation Operator) |
| Observables expressed in terms of creation and annihilation operators | |||
| HSHO | = | ω (a†a + ½) | (Hamiltonian) |
| x | = | (a + a†) / √(2 M ω) | (Coordinate) |
| p | = | –i √(M ω / 2) (a – a†) | (Momentum) |
| Commutators | |||
| [x, p] | = | i | |
| [a, a†] | = | 1 | |
The first classical field we’ll try to “quantise” will consist of complex-valued solutions of the Riemannian Scalar Wave equation. In fact, the “Riemannian Scalar Wave equation” is the Riemannian version of what’s usually known as the Klein-Gordon equation, and virtually every textbook on quantum field theory includes a discussion of the quantisation of the Lorentzian version, either with real-valued solutions[3] or complex-valued solutions[4].
As we’ve discussed previously, the only way to tame the Riemannian wave equations and prevent exponential solutions is to assume that the Riemannian universe is finite in all four dimensions: for example a 4-torus, T4, or a 4-sphere, S4. For simplicity, we will assume a flat 4-torus, but our results will not be tied too much to any specific shape or topology. We described some aspects of electromagnetism in such a universe in this section.
If there are to be any solutions at all to the free (that is, sourceless) RSW equation, the dimensions of the 4-torus Lx, Ly, Lz and Lt must have a special relationship with the maximum frequency, νmax, such that there are integers nx, ny, nz and nt satisfying:
(nx / Lx)2 + (ny / Ly)2 + (nz / Lz)2 + (nt / Lt)2 = νmax2
This allows an integral number of cycles of the wave to occur along each of the dimensions, with the sum of the squares of all the frequencies equal to the required value. For generic values of the dimensions of the torus and νmax there will be no such solutions, but if the dimensions are chosen so that there are solutions, and the universe is extremely large compared to the minimum wavelength, there will be a large but finite number of different integer solutions.
We won’t go into the number theory involved in counting such solutions; we’ll simply assume that there are so many that for most purposes their discrete nature is not experimentally detectable, and also that the directions of the plane waves with the corresponding frequencies are uniformly distributed in all directions. In other words, the possible propagation four-vectors k for the free wave are a finite, discrete set scattered uniformly on a 3-sphere in R4, with radius ωm. We’ll exploit the fact that the set is discrete to make some formulas and calculations simpler, but we’ll also feel free to approximate sums over these vectors with integrals when that’s useful.
We’ll call the set of possible propagation four-vectors for the free wave K4, and write Nmodes for the number of vectors in this set. We’ll choose a particular coordinate across the torus to be our time coordinate, and give the name K3 to the set of projections of the vectors in K4 into the three dimensions excluding t. For each k in K3 there will be two vectors in K4 that project to it, one with a positive time component and one with a negative time component. We’ll call the subset of K4 with positive time components K4+ and the subset with negative time components K4–, and for the sake of simplicitly we’ll assume that there are no modes with a time component of zero. We will refer to the absolute value of the time component as Ek:
Ek = |kt|, for k in K4
Ek = √(ωm2 – |k|2) = √(m2 – |k|2), for k in K3
Here m is the mass of the particle associated with the scalar field, and in our units m = ℏ ωm = ωm = 2π νmax.
To start with, we will write the Riemannian Scalar Wave equation and the corresponding Lagrangian and Hamiltonian in two different forms: the first in terms of a function φ(x, t) of the space and time coordinates, and the second in terms of the (time-dependent) coefficients φk(t) of a mode expansion over certain periodic functions of space.
| Classical Riemannian Scalar Wave Equation | |||
| Four-space coordinate form, complex-valued wave | |||
| 0 | = | ∂μ ∂μ φ(x, t) + m2 φ(x, t) | (Equation of Motion) |
| LRSW | = | ∫ (∂μ φ(x, t)) (∂μ φ*(x, t)) – m2 φ(x, t) φ*(x, t) d3x | (Lagrangian) |
| Π(x, t) | = | ∂t φ*(x, t) | |
| Π*(x, t) | = | ∂t φ(x, t) | (Momenta) |
| HRSW | = | ∫ Π(x, t) Π*(x, t) – (∂i φ(x, t)) (∂i φ*(x, t)) + m2 φ(x, t) φ*(x, t) d3x | (Hamiltonian) |
| Mode expansion form k is in K3 | |||
| fk(x) | = | √(1/V) exp(–i k · x) | |
| φ(x, t) | = | Σk in K3 φk(t) fk(x) | (Mode Expansion) |
| ∂t2 φk(t) | = | –Ek2 φk(t) | (Equation of Motion) |
| LRSW | = | Σk in K3( ∂t φk(t) ∂t φ*k(t) – Ek2 φk(t) φ*k(t) ) | (Lagrangian) |
| Πk(t) | = | ∂t φ*k(t) | |
| Π*k(t) | = | ∂t φk(t) | (Momenta) |
| HRSW | = | Σk in K3( Πk(t) Π*k(t) + Ek2 φk(t) φ*k(t) ) | (Hamiltonian) |
In the first set of equations, we are treating φ(x, t) and its complex conjugate φ*(x, t) as two independent fields, and the Lagrangian density LRSW(x) (the quantity we integrate over space to get the total Lagrangian) yields the equation of motion directly via the Euler-Lagrange equation for the complex conjugate field:
∂μ (∂∂μ φ*(x, t) LRSW(x)) = ∂φ*(x, t)LRSW(x)
∂μ ∂μ φ(x, t) = – m2 φ(x, t)
The momenta associated with the field and its complex conjugate are defined as the derivative of the Lagrangian density with respect to the time derivative of those two fields:
Π(x, t) = ∂∂t φ(x, t) LRSW(x) = ∂t φ*(x, t)
Π*(x, t) = ∂∂t φ*(x, t) LRSW(x) = ∂t φ(x, t)
The Hamiltonian density is found by taking the sum over the two fields, φ(x, t) and its complex conjugate, of the product of the momentum and the time derivative of the field, and then subtracting the Lagrangian density:
HRSW(x) = Π(x, t) ∂t φ(x, t) + Π(x, t)* ∂t φ(x, t)* – LRSW(x)
= 2 Π(x, t) Π(x, t)* – LRSW(x)
In the formula for the Hamiltonian shown in the table, the repeated index i is summed over space coordinates only, with the time derivatives accounted for by the momenta.
Next, we write φ(x, t) as a finite sum of periodic functions of space, fk(x), proportional to exp(–i k · x) for each k in K3. We call the coefficients in this expansion φk(t). We normalise the fk with a factor √(1/V), where V is the volume of space across the four-torus, V = Lx Ly Lz, so that:
∫ fk(x) fq*(x) d3x = δk,q
The new Lagrangian in terms of the mode coefficients φk(t) and their complex conjugates is found by substituting the mode expansion into the original integral for LRSW, then making use of the orthogonality of the mode functions. The sum of the squares of the spatial derivatives for each mode is just k2, which combines with the m2 term to give Ek2. The formulas for the momenta and the Hamiltonian can then be found from the Lagrangian.
Each term in the mode coefficient version of the Hamiltonian almost matches the form of the Hamiltonian of a simple harmonic oscillator, but these degrees of freedom φk(t) and φ*k(t) and their associated momenta are complex numbers, whereas the position and momentum of a simple harmonic oscillator are real numbers. So we need to translate the Hamiltonian into a function of real-valued degrees of freedom. This isn’t hard: each term is a product of a complex number and its conjugate, which equals the absolute value of that complex number squared, which equals the sum of the squares of the real part and the imaginary part (where we construe the imaginary part as real, i.e. we divide out the factor of i). So we can rephrase everything in terms of:
Rek(t) = Re φk(t)
Imk(t) = [ Im φk(t) ] / i
After doing this first in the Lagrangian we can compute the associated momenta, then we end up with a Hamiltonian that takes precisely the harmonic oscillator form, with two real degrees of freedom for every mode.
| Classical Riemannian Scalar Wave Equation | |||
| Real-valued degrees of freedom: Rek(t) and Imk(t)
k is in K3 | |||
| φk(t) | = | Rek(t) + i Imk(t) | (Real Variables) |
| ∂t2 Rek(t) | = | –Ek2 Rek(t) | |
| ∂t2 Imk(t) | = | –Ek2 Imk(t) | (Equations of Motion) |
| LRSW | = | Σk in K3( (∂t Rek(t))2 – Ek2 Rek(t)2 + (∂t Imk(t))2 – Ek2 Imk(t)2 ) | (Lagrangian) |
| ΠRe k(t) | = | 2 ∂t Rek(t) | |
| ΠIm k(t) | = | 2 ∂t Imk(t) | (Momenta) |
| HRSW | = | Σk in K3( ¼ ΠRe k(t)2 + Ek2 Rek(t)2 + ¼ ΠIm k(t)2 + Ek2 Imk(t)2 ) | (Hamiltonian) |
If we compare each term in the Hamiltonian in the last line of this table with the Hamiltonian for the simple harmonic oscillator, we see that we can make the two match up precisely by putting the harmonic oscillator particle’s mass M equal to 2 (this M has nothing to do with the mass of the particle we’re describing with our scalar field), putting the harmonic oscillator frequency ω equal to Ek for each of our modes, and identifying the harmonic oscillator’s coordinate x with either Rek or Imk and the harmonic oscillator’s momentum p with either ΠRe k or ΠIm k. We then define creation and annihilation operators for every k for both the real and imaginary degrees of freedom.
| Quantised Riemannian Scalar Field | |||
| Real-valued degrees of freedom: Rek and Imk
k is in K3 | |||
| aRe k | = | i / (2 √(Ek)) (ΠRe k – 2 i Ek Rek) | |
| aIm k | = | i / (2 √(Ek)) (ΠIm k – 2 i Ek Imk) | (Annihilation Operators) |
| aRe k† | = | –i / (2 √(Ek)) (ΠRe k + 2 i Ek Rek) | |
| aIm k† | = | –i / (2 √(Ek)) (ΠIm k + 2 i Ek Imk) | (Creation Operators) |
| Observables expressed in terms of creation and annihilation operators | |||
| HRSW | = | Σk in K3( Ek (aRe k†aRe k + aIm k†aIm k + 1) ) | (Hamiltonian) |
| Rek | = | (aRe k + aRe k†) / (2 √(Ek)) | |
| Imk | = | (aIm k + aIm k†) / (2 √(Ek)) | (Coordinates) |
| ΠRe k | = | –i √(Ek) (aRe k – aRe k†) | |
| ΠIm k | = | –i √(Ek) (aIm k – aIm k†) | (Momenta) |
| Commutators | |||
| [Rek, ΠRe q] | = | i δk,q | |
| [aRe k, aRe q†] | = | δk,q | |
| [Imk, ΠIm q] | = | i δk,q | |
| [aIm k, aIm q†] | = | δk,q | |
The creation and annihilation operators here work in exactly the same way as those for the simple harmonic oscillator: the creation operators aRe k† and aIm k† turn eigenstates of the Hamiltonian with energy E into new eigenstates with energy E+Ek, while the annihilation operators aRe k and aIm k turn eigenstates with energy E into new eigenstates with energy E–Ek. We define the ground state ψ0 of the system to be the vector such that:
aRe k ψ0 = 0
aIm k ψ0 = 0
for every k in K3. Combining these equations with the Hamiltonian, we see that the energy of ψ0 is:
E0 = Σk in K3 Ek
≈ [½Nmodes / π2] ∫γ=0π/2 m cos(γ) 4 π sin(γ)2 dγ
= 2 Nmodes m / (3 π)
where the approximation comes from treating the ½Nmodes vectors in K3 as the projection of a continuum of vectors uniformly distributed on the t > 0 half of a three-sphere of radius m. In the Lorentzian case, E0 is infinite and needs to be subtracted out by defining it as the zero of a new energy scale; this sounds questionable, but since differences in energy, rather than actual values, are what matters in most of quantum mechanics it works well enough. In our case we don’t really need to do that, and whether or not we include E0 when describing the energies of quantum states, the specific value it takes will show up in some formulas in its own right.
The separate modes of the field – for the various vectors k in K3 and for the real and imaginary parts – act just like completely independent harmonic oscillators. In quantum mechanics, independent systems are described by a Hilbert space that is the tensor product of the Hilbert spaces for the individual systems, so we can think of the Hilbert space for our field as a tensor product of Nmodes copies of the harmonic oscillator Hilbert space. All the operators that are indexed with Re k or Im k act only on their particular factor of the whole Hilbert space, and act as the identity on all the other factors. Nothing in any mode messes with what’s going on in any other mode.
That’s very unrealistic, of course, because the electromagnetic and Dirac-type fields we ultimately want to deal with are coupled to each other. But treating a sourceless field is a useful warm-up exercise before tackling harder problems.
Having found degrees of freedom that we could quantise by analogy with the harmonic oscillator, we’re now going to translate everything back to our original, complex-valued degrees of freedom, which are easier to interpret physically. The relationship between the real and complex degrees of freedom is already fixed; that doesn’t quite tell us how to define creation and annihilation operators for the complex-valued modes, but we can check that the choices here give the correct commutators and put the Hamiltonian into the right form. (Though it might have been more straightforward to put ak = (1/√2) (aRe k + i aIm k) and bk = (1/√2) (aRe k – i aIm k) rather than the versions below in which the right-hand sides have been multiplied by an extra factor of –i, these phases have been chosen to give field variables that agree with Weinberg[4] for ease of comparison.)
| Quantised Riemannian Scalar Field | |||
| Complex-valued degrees of freedom: φk and φk†
k is in K3 | |||
| ak | = | (1/√2) (aIm k – i aRe k) | |
| = | 1 / √(2Ek) (Πk† – i Ek φk) | ||
| bk | = | –(1/√2) (aIm k + i aRe k) | |
| = | 1 / √(2Ek) (Πk – i Ek φk†) | (Annihilation Operators) | |
| ak† | = | (1/√2) (aIm k† + i aRe k†) | |
| = | 1 / √(2Ek) (Πk + i Ek φk†) | ||
| bk† | = | –(1/√2) (aIm k† – i aRe k†) | |
| = | 1 / √(2Ek) (Πk† + i Ek φk) | (Creation Operators) | |
| Observables expressed in terms of creation and annihilation operators | |||
| HRSW | = | Σk in K3( Ek (ak†ak + bk†bk + 1) ) | (Hamiltonian) |
| φk | = | i (ak – bk†) / √(2Ek) | |
| φk† | = | –i (ak† – bk) / √(2Ek) | (Coordinates) |
| Πk | = | √(Ek/2) (ak† + bk) | |
| Πk† | = | √(Ek/2) (ak + bk†) | (Momenta) |
| Commutators | |||
| [φk, Πq] | = | i δk,q | |
| [ak, aq†] | = | δk,q | |
| [φk†, Π†q] | = | i δk,q | |
| [bk, bq†] | = | δk,q | |
Now φk and Πk are non-Hermitian operators on our Hilbert space, rather than complex-valued functions of time, and the operators associated with the complex conjugates of those functions are the Hermitian adjoints φk† and Πk†. We normally think of observables as being Hermitian operators, but that’s only true if they’re measuring real-valued quantities, and these non-Hermitian operators are perfectly good observables for the complex-valued mode coefficients we introduced for the classical field.
In place of the operators for the two kinds of real-valued degrees of freedom, we now have annihilation operators we’ve named ak and bk, and their Hermitian adjoints as the creation operators. The Hamiltonian takes exactly the same form in terms of these new operators as it did for the old ones, so again we will have a ground state ψ0 with the energy E0. And as before, operating on an energy eigenstate with either of the creation operators ak† or bk† will give a new eigenstate with its energy increased by Ek.
What is the physical meaning of the states we get when we add a quantum of energy to the ground state with ak† or bk†? To answer that, we need to look back to the Lagrangian for the classical field, expressed in terms of the complex mode coefficients:
LRSW = Σk in K3( ∂t φk(t) ∂t φ*k(t) – Ek2 φk(t) φ*k(t) )
If we multiply every φk by a phase, exp(–i α), each φ*k is multiplied by exp(i α) and the Lagrangian itself is unchanged. So uniformly rotating the phase of the entire field is a symmetry of the Lagrangian. Any symmetry of this kind gives us a conserved quantity, and the version of Noether’s Theorem that applies to discrete variables tells us that the quantity is:
C = Σk in K3( (∂∂t φk LRSW) (∂α exp(–i α) φk(t))|α=0 + (∂∂t φ*k LRSW) (∂α exp(i α) φ*k(t))|α=0 )
= –i Σk in K3( (∂t φ*k(t)) φk(t) – (∂t φk(t)) φ*k(t) )
= –i Σk in K3( Πk(t) φk(t) – Π*k(t) φ*k(t) )
If we translate C into an operator expressed in terms of the creation and annihilation operators, we get:
C = Σk in K3( ak† ak – bk†bk )
Using an argument much like that we used to find the energy eigenstates, it’s easy to show that ak† ak counts the number of quanta that have been added to the ground state with ak†, i.e.
(ak† ak) ψ0 = 0
(ak† ak) (ak†)n ψ0 = n (ak†)n ψ0
Similarly, the operator bk†bk counts the number of quanta that have been added to the ground state with bk†:
(bk† bk) (bk†)n ψ0 = n (bk†)n ψ0
The difference of the two, summed over all k, is thus the total number of quanta created with a† operators minus the total number created with b† operators. This number is conserved; we can check that this holds true in the quantum version by checking that C commutes with the Hamiltonian. (In fact, the two number operators are individually conserved, but that’s because we’re dealing with a free field theory where nothing much happens. The difference of the number operators, arising as it does from a uniform change in the phase of φ, will be conserved even in an interacting field theory, so long as the interaction term has factors of both φ and φ*.)
What this is telling us is that the ak† operators are creating particles and the bk† operators the corresponding antiparticles, in the sense that these two kinds of quanta have a “charge” associated with them that is opposite in the two cases, and whose net value remains unchanged over time. If φ was coupled to the electromagnetic field this would be an electric charge, but at this point it’s just a conserved quantum number with no wider meaning. For the most general energy eigenstate ψ, we have:
ψ = (ak1†)q1 (ak2†)q2 (ak3†)q3 ... (bk1†)n1 (bk2†)n2 (bk3†)n3 ... ψ0
H ψ = (E0 + (q1 + n1) Ek1 + (q2 + n2) Ek2 + (q3 + n3) Ek3 + ... ) ψ
C ψ = ((q1 + q2 + q3 + ...) – (n1 + n2 + n3 + ... )) ψ
In retrospect, we can now see what kind of quanta the operators aRe k† and aIm k† were creating: they were equal combinations of the particle and antiparticle states, with no net charge!
In the Lorentzian universe, observers in relative motion will agree about the classification of states into particles and antiparticles, but that’s not true in the Riemannian universe. Suppose k is a three-vector such that Ek is quite small; this means the four-vector k = (Ek, k) will be pointing in an almost spatial direction, in the frame in which these quantities are being measured, and it won’t take much relative motion for another observer to give it a negative time component.
We can write things in a less frame-bound way by defining an annihilation operator indexed by the four-vectors in K4:
| c(E, k) | = |
|
with the corresponding creation operator equal to its Hermitian adjoint:
| c(E, k)† | = |
|
Whether the state c(E, k)† ψ0 is seen as a particle or an antiparticle in the frame in which we’re working, if we look at another physical system related to the original one by an arbitrary four-space rotation R it will be described by the state cR (E, k)† ψ0.
In terms of these operators, by indexing everything with four-vectors in K4 we can encompass both particle and antiparticle states in one sweep. The modes and momenta where we previously specified Hermitian adjoints separately can now be found by negating the four-vector index, with φ(–Ek, –k) in our new definition taking the place of φk†.
| Quantised Riemannian Scalar Field | |||
| Complex-valued degrees of freedom: φk k is now a four-vector from K4 | |||
| ck | = | 1 / √(2Ek) (Π–k – i Ek φk) | (Annihilation Operators) |
| ck† | = | 1 / √(2Ek) (Πk + i Ek φ–k) | (Creation Operators) |
| Observables expressed in terms of creation and annihilation operators | |||
| φk | = | i (ck – c–k†) / √(2Ek) | (Coordinates) |
| Πk | = | √(Ek/2) (ck† + c–k) | (Momenta) |
| HRSW | = | Σk in K3( Πk Π†k + Ek2 φk φ†k ) | |
| = | Σk in K4( Ek (ck†ck + ½) ) | (Hamiltonian) | |
| Commutators | |||
| [φk, Πq] | = | i δk,q | |
| [ck, cq†] | = | δk,q | |
Now that we have operators for the variables associated with the modes, let’s see what their expectation values are for some states of the quantised field. In order to calculate expectation values we’ll need to know the inner products between various states, and we’ll start by assuming that the ground state ψ0 is normalised:
< ψ0, ψ0 > = 1
What about the state ψq = cq† ψ0, where we’ve put one quantum into the field for some mode q in K4?
< ψq, ψq >
= < cq† ψ0, cq† ψ0 >
= < ψ0, cq cq† ψ0 >
= < ψ0, (cq† cq + 1) ψ0 >
= < ψ0, ψ0 >
= 1
Here we’ve made use of a general property of adjoints and inner products, < A x, y > = < x, A† y >, the commutator between the annihilation and creation operators, and the fact that any annihilation operator applied to the ground state gives zero.
For the moment we’re going to gloss over the fact that either these states (in the Schrödinger picture), or the operators (in the Heisenberg picture) should be seen as varying over time; in the cases we’re looking at here the time variation amounts to an oscillating phase that has no effect on the expectation values.
The expectation value of φk for the state ψq is:
< ψq, φk ψq >
= < cq† ψ0, φk cq† ψ0 >
= < ψ0, cq φk cq† ψ0 >
= [i / √(2Ek)] < ψ0, cq (ck – c–k†) cq† ψ0 >
= 0
This must be zero, because no odd number of creation and annihilation operators can bring the ground state back to the ground state. What’s more, it shouldn’t surprise us that this expectation value is zero, because it’s a bit like asking for the mean position of the particle in a simple harmonic oscillator, which will of course be x = 0. But the position squared should have a non-zero average, or in the case of this complex field amplitude, the expectation value of φk† φk (which we can also write as φ–k φk) should be non-zero.
We’ll compute this first for the ground state. Note that φk and φk† commute, so the order in which we write these operators makes no difference.
< ψ0, φ–k φk ψ0 >
= < ψ0, (i (c–k – ck†) / √(2Ek)) (i (ck – c–k†) / √(2Ek)) ψ0 >
= –< ψ0, (c–k – ck†) (ck – c–k†) ψ0 > / (2Ek)
= 1 / (2Ek)
Now for the state ψq:
< ψq, φ–k φk ψq >
= < ψ0, cq φ–k φk cq† ψ0 >
= –< ψ0, cq (c–k – ck†) (ck – c–k†) cq† ψ0 > / (2Ek)
= (1 + δq, k + δq, –k) / (2Ek)
The squared momenta associated with the modes have expectation values that differ from these only by a factor of Ek2.
< ψ0, Π–k Πk ψ0 > = Ek / 2
< ψq, Π–k Πk ψq > = [Ek / 2] (1 + δq, k + δq, –k)
What we’re seeing here is that these squared-amplitude and squared-momentum observables are sensitive to ground-state energy: they will give us non-zero expectation values even when the state of the field has no quanta in the mode the observable is tuned to. And energy eigenstates such as ψq are highly non-classical: the energy is sharply defined at the expense of a completely indeterminate phase for the mode.
Though we won’t go into the details, it’s worth briefly sketching how a semi-classical state for the field could be constructed. In the simple harmonic oscillator, you can take the ground state wave function – a Gaussian wave packet – and displace its centre any distance you like from the centre of the energy well. The translated wave now contains components from an infinite number of energy eigenfunctions, but as they evolve over time the wave packet simply moves back and forth in the well, without changing its shape, very much like a classical particle [2].
We can do something similar with one of the modes of our complex scalar field, and if we work with the real and imaginary parts it’s easy to mimic the harmonic oscillator construction. By setting up Gaussian wave packets in the real and imaginary parts that are oscillating 90 degrees out of phase, the result is a complex mode amplitude that rotates in the complex plane: a two-dimensional Gaussian circling the origin at a constant distance. For a large enough squared amplitude, this state will resemble a classical wave with a well-defined phase.
In Lorentzian quantum field theory, the normal development of the subject involves writing the field φ, its Hermitian adjoint, and their conjugate momenta as operator-valued functions of the space coordinates, using the original spatial modes and the quantised mode coefficient operators. That can be done in the Riemannian case too, but the result has to be treated with caution – because φ(x) defined that way will involve a sum over K3, making it dependent on the observer’s choice of a t coordinate. The Lorentzian equivalent, which is an integral over all propagation vectors on the positive mass hyperboloid (the set of timelike vectors such that k · k = –m2 and kt > 0), is only tied to a choice of an overall sign for the time coordinate, and transforms sensibly between observers in relative motion. But a Riemannian field φ(x) is locked to a specific choice of time axis, because observers with even slightly different time axes will disagree as to what is a particle and what is an antiparticle.
There is another problem that complicates the Riemannian case, and we can see this even in the classical version. Ideally, we’d like the change of variables between the field at each point in space and the mode coefficients to be a canonical transformation. In Hamiltonian mechanics, we define the Poisson bracket as a differential operator on pairs of functions:
{f, g}PB = (∂qj f ) (∂pj g) – (∂pj f ) (∂qj g)
where we’re summing over the repeated index j. The coordinates qi and momenta pi have the Poisson brackets:
{qi, qk}PB = 0
{pi, pk}PB = 0
{qi, pk}PB = δik
For continuous degrees of freedom such as field values, the discrete indices are replaced by spatial coordinates, the sums by integrals, and the Kronecker delta is replaced by a Dirac delta function. In a canonical transformation between variables, these equations should hold for the new set of coordinates and momenta when the Poisson brackets are defined in terms of the original variables[5]. Explicitly, if the new coordinates are Qi and the new momenta Pi, we should have:
{Qi, Qk}PB = (∂qj Qi) (∂pj Qk) – (∂pj Qi) (∂qj Qk) = 0
{Pi, Pk}PB = (∂qj Pi) (∂pj Pk) – (∂pj Pi) (∂qj Pk) = 0
{Qi, Pk}PB = (∂qj Qi) (∂pj Pk) – (∂pj Qi) (∂qj Pk) = δik
Things get a little trickier when one set of variables are continuous and the other discrete, but in some cases everything still works perfectly. For example, if we were expanding over the countably infinite set of Fourier modes of the field that met periodic boundary conditions on space alone, with suitable normalisation we would get a Kronecker delta in these equations when we changed from spatial coordinates to mode coefficients (with the sum over the index j replaced by an integral over the spatial coordinates), and a Dirac delta function when we performed the reverse transformation.
In the present case, though, what do we get? The new coordinates and momenta in terms of the old are:
φ(x, t) = Σk in K3 φk(t) fk(x)
Π(x, t) = ∂t φ*(x, t) = Σk in K3 (∂t φ*k(t)) fk*(x) = Σk in K3 Πk(t) fk*(x)
so we have the partial derivatives between old and new variables (where for brevity we’ll now suppress the explicit time-dependence):
∂φk φ(x) = fk(x)
∂Πk Π(x) = fk*(x)
and the Poisson bracket between coordinates and momenta:
{φ(x), Π(y)}PB
= Σk in K3( (∂φk φ(x)) (∂Πk Π(y)) – (∂Πk φ(x)) (∂φk Π(y)) )
= Σk in K3 fk(x) fk*(y)
= (1/V) Σk in K3 exp(i k · (y – x))
= (1/V) Σk in K4+ exp(i k · (y – x))
≈ [Nmodes/(2 π2 V)] ∫u over S3+ exp(i m u · (y – x))
where in the second-last line we’ve used the fact that x and y are purely spatial, so it makes no difference whether we take their dot product with some k in K3 or the k in K4+ that projects to it, and in the last line we approximate the sum over the vectors in K4+ as an integral over the positive half of the unit three-sphere in R4. We can exploit the fact that this integral will be invariant under rotations of three-space to choose coordinates such that y – x = |x – y| ez. In polar coordinates (γ, θ, φ) on S3+, we have 0 < γ < π/2, 0 < θ < π, and 0 < φ < 2π, the measure is sin(γ)2 sin(θ), and the unit four-vector u is:
u = (cos(γ), sin(γ) sin(θ) cos(φ), sin(γ) sin(θ) sin(φ), sin(γ) cos(θ))
So the dot product we need is:
u · (|x – y| ez) = |x – y| sin(γ) cos(θ)
Since the integrand is independent of the azimuthal coordinate φ (not to be mistaken for the field amplitude), we can integrate that out immediately, leaving:
{φ(x), Π(y)}PB
≈ [Nmodes/(π V)] ∫θ=0π ∫γ=0π/2 exp(i m |x – y| sin(γ) cos(θ)) sin(γ)2 sin(θ) dγ dθ
= [2 Nmodes/(π V)] [1 / (m |x – y|)] ∫γ=0π/2 sin(m |x – y| sin(γ)) sin(γ) dγ
= [Nmodes/V] J1(m |x – y|) / (m |x – y|)
Here J1 is a Bessel function of the first kind. J1 is roughly cyclic, and is zero at the origin, but when we divide through by its argument we get a function that peaks at the origin and then dies away, while oscillating. The first zero occurs when m |x – y| ≈ 4, and when we recall that m = ωm we see that the width of the peak is of the same order as the minimum wavelength associated with the RSW equation. But although this function has a peak, it certainly isn’t a Dirac delta function, so we do not have a canonical transformation of variables.
The problem is that the modes available to us can’t be combined to produce a perfectly localised field. This has nothing to do with quantum mechanics, and it isn’t because the set of modes is finite; even when we pretend we have a continuum of modes with propagation vectors spread across half a three-sphere, there is still a minimum wavelength to those modes, and we can’t expect to build a function from them with an arbitrarily narrow peak.
So instead of trying to deal with the field’s value at every single point, it makes more sense to find a new basis for the space spanned by the mode functions fk(x), consisting of new functions that are as localised as possible, given that they belong to that space.
Let’s define a set of functions gχ(x) as:
gχ(x) = Σk in K3 √(Ek/E0) fk(x–χ)
= Σk in K3 √(Ek/E0) exp(i k · χ) fk(x)
where χ for the moment is any three-vector. Any gχ is a linear combination of the mode functions fk, so unlike a Dirac delta function it lies in the subspace of functions we can actually construct. We can approximate g0 using an integral:
g0(x) = Σk in K3 √(Ek/E0) fk(x)
≈ [Nmodes/(2 π2 √(V E0))] ∫u over S3+ exp(–i m u · x) √(m ut)
= √[3 Nmodes/(2 π V)] ∫θ=0π ∫γ=0π/2 exp(–i m |x| sin(γ) cos(θ)) sin(γ)2 (√cos(γ)) sin(θ) dγ dθ
= √[6 Nmodes/(π V)] / (m|x|) ∫γ=0π/2 sin(m |x| sin(γ)) (sin(γ) √(cos(γ)) dγ
= √[3 Nmodes/V][Γ(3/4)/21/4] J5/4(m |x|) / (m |x|)5/4
This Bessel function divided by a power of its argument gives a very similar shape to the function we found for the Poisson bracket, with a peak whose width is of the same order as the minimum wavelength. So it’s a reasonably localised function, and we wouldn’t expect to be able to do much better with any linear combination of the modes.
Now, the function gχ(x) = g0(x – χ) just translates this peak from the origin to another location, so all functions of this kind will be equally localised in space. We will now assume that it’s possible to choose a set of ½Nmodes different points χ such that all the gχ are mutually orthogonal; we’ll call that choice of points Χ. If we normalise these functions, they will then comprise an alternative orthonormal basis for the function space spanned by the fk.
What if that assumption isn’t true? Well, we do know that if we chose any distinct ½Nmodes points χ, the gχ would still give us a basis for the function space. We could then turn that basis into an orthonormal basis with the Gram-Schmidt orthogonalisation process. The resulting functions would no longer all take the form gχ(x), but if we’d scattered our points uniformly in space the result should still be a set of localised functions qualitatively very much like the gχ.
Since the fk certainly are orthogonal, the assumption of orthogonality for the gχ is equivalent to:
< gχ1, gχ2> = Σk in K3 (Ek/E0) exp(i k · (χ2 – χ1)) = δχ1, χ2 [Σk in K3 (Ek/E0)] = δχ1, χ2
In place of φ(x), the field at an arbitrary point, we will write φχ for the coefficient of gχ(x) in the field:
Σk in K3 φk fk(x) = Σχ in Χ φχ gχ(x)
Using the orthonormality of the gχ, we can extract one coefficient by taking the inner product with the corresponding gχ, giving us:
φχ = Σk in K3 √(Ek/E0) exp(–i k · χ) φk
The inverse formula is:
φk = Σχ in Χ √(Ek/E0) exp(i k · χ) φχ
From these formulas and the orthogonality assumption, it’s not hard to show that the transformation of the classical variables from the mode coefficients φk to the spatial coefficients φχ is a canonical transformation:
{φχ1, Πχ2}PB = δχ1, χ2
We can now write the operators corresponding to these new variables, simply by using the operator form of the φk.
| Quantised Riemannian Scalar Field Schrödinger picture | |||
| The vector χ is a spatial three-vector from the set Χ. The operators are unchanging over time, and apply to a time-dependent state vector. | |||
| φχ | = | Σk in K3 √(Ek/E0) exp(–i k · χ) φk | |
| = | i/√(2E0) Σk in K4+ (ck – c–k†) exp(–i k · χ) | ||
| φχ† | = | Σk in K3 √(Ek/E0) exp(i k · χ) φk† | |
| = | i/√(2E0) Σk in K4– (ck – c–k†) exp(–i k · χ) | ||
| Inverse formula for plane-wave mode coefficients. | |||
| φk | = | Σχ in Χ √(Ek/E0) exp(i k · χ) φχ | |
| Orthogonality assumption for χ in Χ. | |||
| Σk in K3 Ek exp(i k · (χ2 – χ1)) | = | δχ1, χ2 E0 | |
In writing the sums indexed by four-vectors in K4+ and K4–, we’ve made use of the fact that the dot product of the purely spatial vector χ with these four-vectors is the same as the dot product with their projection in K3, and in writing the second form for the Hermitian adjoint φχ†, we’ve changed the indexing vector from k in K4+ to its opposite in K4–.
You’ll note that the factor of 1/√Ek that’s present in the operators for the mode coefficients cancels out in these spatially localised operators. The reason for inserting a factor of √Ek into the definition of the functions gχ was precisely to achieve this cancellation! The equivalent formulas in the Lorentzian theory are integrals over all spatial three-vectors, and they need the factor of 1/√Ek in order to ensure that certain products turn out to be Lorentz-invariant – a factor of 1/Ek being exactly what’s needed to make an integral over spatial vectors into a Lorentz-invariant integral over the mass hyperboloid. But our sum is over four-vectors that are already uniformly distributed over half the three-sphere, so we don’t want any functions of the frame-dependent energy hanging around making it harder to formulate SO(4)-invariant quantities.
This field of operators is defined in the Schrödinger picture, where some operators are considered to be fixed for all time (like the operators x and p in our original harmonic oscillator), and the state vector changes over time. But in quantum field theory it’s more common to use the Heisenberg picture, where the state vector is taken to be fixed for all time, and all operators become functions of time.
To make the switch to the Heisenberg picture, if the state ψ is to be fixed at ψ(0), operators need to change with time according to:
A(t) = exp(i H t) A(0) exp(–i H t)
Now, let’s consider the specific case of an annihilation operator ak and our Hamiltonian HRSW. Apart from the term Ek ak†ak, the operator ak commutes with everything else in HRSW, so we have:
[ak, HRSW] = [ak, Ek ak†ak] = Ek [ak, ak†] ak
ak HRSW – HRSW ak = Ek ak
which gives us:
HRSW ak = ak (HRSW – Ek)
HRSWn ak = ak (HRSW – Ek)n
Treating the exponential of the Hamiltonian as a power series, this tells us that:
exp(i HRSW t) ak = ak exp(i (HRSW – Ek) t)
exp(i HRSW t) ak exp(–i HRSW t) = ak exp(–i Ek t)
Taking the Hermitian adjoint of both sides of this equation yields the transformation property for the corresponding creation operator:
exp(i HRSW t) ak† exp(–i HRSW t) = ak† exp(i Ek t)
Obviously the bk and bk† transform in the same way. All our c operators are just a or b renamed, and so long as we are clear that Ek is the absolute value of the time component associated with a four-vector k in K4, the same rules apply to ck and ck† as well. Using these transformation rules, we can write our field operators and the associated momenta in the Heisenberg picture, as functions of both space and time.
| Quantised Riemannian Scalar Field Heisenberg picture | |||
| The vector χ is a spatial three-vector from the set Χ. The operators are time-dependent, and apply to an unchanging state vector. | |||
| φχ(t) | = | i/√(2E0) Σk in K4+ (ck exp(–i Ek t) – c–k† exp(i Ek t)) exp(–i k · χ) | |
| φχ†(t) | = | i/√(2E0) Σk in K4– (ck exp(–i Ek t) – c–k† exp(i Ek t)) exp(–i k · χ) | (Coordinates) |
| Πχ(t) | = | ∂t φχ†(t) | |
| = | 1/√(2E0) Σk in K4– Ek (ck exp(–i Ek t) + c–k† exp(i Ek t)) exp(–i k · χ) | ||
| = | 1/√(2E0) Σk in K4+ Ek (c–k exp(–i Ek t) + ck† exp(i Ek t)) exp(i k · χ) | ||
| Πχ†(t) | = | ∂t φχ(t) | |
| = | 1/√(2E0) Σk in K4+ Ek (ck exp(–i Ek t) + c–k† exp(i Ek t)) exp(–i k · χ) | ||
| = | 1/√(2E0) Σk in K4– Ek (c–k exp(–i Ek t) + ck† exp(i Ek t)) exp(i k · χ) | (Momenta) | |
Let’s look at some expectation values for the operators φχ(t). Since they are linear combinations of the mode amplitudes they will have some properties in common with them: the expectation value of each operator itself on states such as ψ0 and ψq will be zero. So once again we’ll look at the squared amplitude, which we get from φχ†(t) φχ(t).
< ψ0, φχ†(t) φχ(t) ψ0 >
= Nmodes / (4E0)
≈ 3π / (8m)
So as with the mode amplitudes, these spatial coefficient operators are sensitive to the ground-state energy. For a state with one quantum in mode q, we have:
< ψq, φχ†(t) φχ(t) ψq >
= (Nmodes + 2) / (4E0)
≈ 3π (1 + 2/Nmodes) / (8m)
So the spatial coefficient is completely blind to which single-quantum plane-wave mode is present, and can barely distinguish these states from the ground state.
None of that’s too surprising; what we expect these spatial operators to be sensitive to is the difference between spatially localised states. We could construct an orthonormal set of spatially localised states by mimicking the way we constructed the spatially localised modes gχ from the plane-wave modes fk, defining the states ψχ by:
Maybe ψχ = Σk in K3 √(Ek/E0) exp(i k · χ) ψk?
However, these states don’t give simple expectation values for the squared spatial coefficient operators, and there’s no easy way to construct SO(4)-invariant quantities from them. But it turns out that we can get some useful localised states by applying the spatial coefficient operators themselves to the ground state:
ψ(+)χ, t = 2 √(E0/Nmodes) φχ†(t) ψ0 = –i √(2/Nmodes) Σk in K4+ exp(i (Ek t + k · χ)) ψk
ψ(–)χ, t = 2 √(E0/Nmodes) φχ(t) ψ0 = –i √(2/Nmodes) Σk in K4– exp(i (Ek t + k · χ)) ψk
The intention here is that the state is localised around the three-vector χ at the specific time t, and can be expected to spread out spatially at other times; the superscript (±) specifies a particle or antiparticle.
Let’s compute the inner products between the particle states:
< ψ(+)χ1, t1, ψ(+)χ2, t2 >
= (4E0/Nmodes) < ψ0, φχ1(t1) φχ2†(t2) ψ0 >
= (2/Nmodes) Σk in K4+ exp(i (Ek (t2–t1) + k · (χ2 – χ1)))
= (2/Nmodes) Σk in K4+ exp(i (kt (t2–t1) + k(3) · (χ2 – χ1)))
= (2/Nmodes) Σk in K4+ exp(i k · δ)
where we have defined the four-vector:
δ = (t2–t1, χ2 – χ1)
The states for different χ and/or t are not orthogonal, but the inner product will peak when the location and time are identical and undergo a J1(m |χ2 – χ1|) / (m |χ2 – χ1|) fall-off as the separation in space increases.
Between the antiparticle states we have:
< ψ(–)χ1, t1, ψ(–)χ2, t2 >
= (4E0/Nmodes) < ψ0, φχ1†(t1) φχ2(t2) ψ0 >
= (2/Nmodes) Σk in K4– exp(i (Ek (t2–t1) + k · (χ2 – χ1)))
= (2/Nmodes) Σk in K4– exp(i ((–kt) (t2–t1) + k(3) · (χ2 – χ1)))
= (2/Nmodes) Σk in K4– exp(i ((–kt) (t2–t1) – k(3) · (χ2 – χ1)))
= (2/Nmodes) Σk in K4– exp(–i k · δ)
In going between the third-last and second-last lines here, we’re using the fact that for every four-vector in K4–, the vector with the opposite spatial part and the same time component is also in K4–. This result is identical to the inner product between particle states.
All the particle and antiparticle states are orthogonal to each other:
< ψ(+)χ2, t2, ψ(–)χ1, t1 > = 0
One of the most important things to know in quantum field theory is the propagator for the field, which gives the amplitude for finding a particle at a certain time and place, say t2 and x2, given that it is definitely present at x1 at time t1. In Lorentzian QFT, this is done in a manner that clearly distinguishes between particles and antiparticles, and can be phrased in a way that respects the usual arrow of time. For example, the Feynman propagator for the events (t1, x1) and (t2, x2) is defined so that if t2 > t1 it is the amplitude for a particle to go from (t1, x1) to (t2, x2), but if t2 < t1 it is the amplitude for an antiparticle to go from (t2, x2) to (t1, x1). In both cases, the amplitude is found by integrating propagation vectors over the positive mass hyperboloid to cover all the different plane waves that could carry the particle or antiparticle from the earlier time to the later. This amplitude is Lorentz-invariant, if you restrict yourself to orthochronous Lorentz transformations: those in which two observers can agree which mass hyperboloid is the positive one, because they agree on the overall positive direction for time.
In Riemannian QFT, the distinction between particles and antiparticles depends on the observer’s state of motion. What’s more, in a T4 universe, in which time is cyclic, it’s meaningless to say that one time comes before another. However, if we drop the part in the description of the Feynman propagator where we switch between two options depending on which event comes first and instead simply add the amplitude for a particle at Event 1 to be detected at Event 2 to the amplitude for an antiparticle at Event 2 to be detected at Event 1, we obtain an SO(4)-invariant quantity:
½ (< ψ(+)χ1, t1, ψ(+)χ2, t2 > + < ψ(–)χ2, t2, ψ(–)χ1, t1 >)
= (2E0/Nmodes) < ψ0, (φχ1(t1) φχ2†(t2) + φχ2†(t2) φχ1(t1)) ψ0 >
= (1/Nmodes) Σk in K4 exp(i k · δ)
≈ 2 J1(m |δ|) / (m |δ|), where δ = (t2–t1, χ2 – χ1)

Clearly this is SO(4)-invariant: it is a function solely of the length of the four-vector δ, a quantity that all observers will agree on. And if we view χ1 and t1 as fixed and treat χ2 and t2 as our coordinates, this is a solution of the sourceless RSW equation with four-rotational symmetry around (t1, χ1).
Of course the Bessel function approximation is just that: an approximation. It has the advantage of perfect SO(4)-invariance and ease of computation, but it doesn’t satisfy the T4 boundary conditions, so if you go around the torus in different directions you’ll end up with different values. In practice, using the shortest four-dimensional distance between any two events will give the appropriate answer.
If we swap our definitions of “particle” and “antiparticle” in the propagator, this amounts to swapping the order of the terms in both inner products, and hence taking the complex conjugate of the whole expression. But since the final value is a real number, this makes no difference. For the same reason, swapping the labels on the two events also makes no difference.
The diagram on the left illustrates what the propagator is measuring. The two events are connected by plane waves with propagation vectors pointing in every possible direction, and there is no invariant meaning to the classification of these waves into particle or antiparticle states.
However, for a given observer we can describe those waves whose propagation vectors point backwards in time as antiparticles travelling forwards in time, and those waves whose propagation vectors point forwards in time as particles, again travelling forwards in time.
Crucially, though, we always include both possibilities. If we followed the Lorentzian prescription for the Feynman propagator and did not include the antiparticle states in this example because some observer had classified Event 1 as coming before Event 2, then even another observer who agreed on that ordering would select a different half-three-sphere of particle states (represented by the red arrows here), and would end up with a different amplitude.
Suppose we repeat the initial steps of the construction we performed when we prepared to quantise a complex scalar field, but in place of the Riemannian scalar wave equation we use the Riemannian Dirac equation. In our earlier discussion of the Dirac equation, we were treating it as describing a quantum wave function, but for our present purposes we will initially pretend that we’re studying a “classical” Dirac field, where the field consists of four complex components and obeys the Dirac equation, but has nothing to do with quantum mechanics. The fields that satisfy this equation form a representation of the Euclidean group; we actually derived the Dirac equation on those terms, in one of the sections on group representations. So initially we’re just mimicking, for this new representation, what we did for the scalar representation previously.
To keep the notation simple, we’ll again refer to the field’s maximum angular frequency (soon to become the particle mass) as m, and the set of possible propagation four-vectors compatible with that mass and the dimensions of the T4 universe as K4, with K3 as the projections of the vectors in K4 to three dimensions and Ek as the unique positive energy associated with any k in K3:
Ek = √(m2 – |k|2)
If we were describing a situation with more than one kind of field, we’d need to distinguish between the different versions of all these things pertaining to each field, since of course there’s no reason why they’d be the same in the various cases.
To expand our Dirac field ψ in Fourier modes, we will make use of the following solutions of the Dirac equation, which generalise the plane wave solutions we discussed earlier:
| Plane Wave Solutions of the Riemannian Dirac Equation in the Weyl Basis | |||
| k is in K3 {ξs} is an orthonormal basis of C2 Hμ are the unit quaternions as matrices (defined here) Sum kjHj ranges over spatial indices x, y, z | |||
| Positive frequency solutions | |||
| ψ+, k, s(x, t) | = | u(k, s) exp(–i (k · x + Ekt)) | (Plane wave) |
| u(k, s) | = | ( [(m+Ek)Ht + kjHj] ξs, [(m+Ek)Ht – kjHj] ξs) / (2 √[m(m+Ek)]) | |
| u(k, s1)† u(k, s2) | = | δs1, s2 | |
| u(k, s1)† γt u(k, s2) | = | δs1, s2 Ek / m | |
| Negative frequency solutions | |||
| ψ–, k, s(x, t) | = | v(k, s) exp(+i (k · x + Ekt)) | (Plane wave) |
| v(k, s) | = | ( [(m+Ek)Ht + kjHj] ξs, –[(m+Ek)Ht – kjHj] ξs) / (2 √[m(m+Ek)]) | |
| v(k, s1)† v(k, s2) | = | δs1, s2 | |
| v(k, s1)† γt v(k, s2) | = | –δs1, s2 Ek / m | |
| Products of u and v spinors | |||
| u(k, s1)† v(k, s2) | = | 0 | |
| v(k, s1)† u(k, s2) | = | 0 | |
| u(k, s1)† γt v(–k, s2) | = | 0 | |
| v(–k, s1)† γt u(k, s2) | = | 0 | |
If you’ve studied the normal, Lorentzian versions of all this, the orthogonality relations will look a bit strange! In Lorentzian QFT, you need to insert γt between any pair of Dirac spinors to get a Lorentz-invariant product, and you have:
u(k, s1)† γt u(k, s2) = δs1, s2 [Lorentzian]
But here, because the rotation group SO(4) has a unitary representation on the Dirac spinors, we can simply take an ordinary inner product between u spinors, or between v spinors, and it will be SO(4)-invariant.
In the mode expansion of the field given below, we extract the purely spatial parts of these two plane-wave solutions ψ±, k, s(x, t) into two sets of functions fk, s(x) and gk, s(x), and then expand a general solution ψ(x, t) as a sum over these functions multiplied by time-dependent coefficients. For ψ(x, t) to be a solution of the Dirac equation, the time-dependent coefficients will satisfy the same equations as the time-dependent parts of ψ±, k, s(x, t), i.e. exp(–i (± Ekt)).
| “Classical” Riemannian Dirac Equation | |||
| Four-space coordinate form Sum γj ∂j ranges over spatial indices x, y, z | |||
| 0 | = | i γμ ∂μ ψ(x, t) – m ψ(x, t) | (Equation of Motion) |
| LRD | = | ∫ ψ†(x, t) (i γμ ∂μ ψ(x, t) – m ψ(x, t)) d3x | (Lagrangian) |
| Π(x, t) | = | i ψ†(x, t) γt | |
| Π†(x, t) | = | 0 | (Momenta) |
| HRD | = | ∫ ψ†(x, t) (–i γj ∂j ψ(x, t) + m ψ(x, t)) d3x | (Hamiltonian) |
| Mode expansion form k is in K3, s is spin ±½ | |||
| fk, s(x) | = | √(1/V) u(k, s) exp(–i k · x) | |
| gk, s(x) | = | √(1/V) v(k, s) exp(+i k · x) | (Spatial modes) |
| ψ(x, t) | = | Σk in K3, s=±½ (Ak, s(t) fk, s(x) + Bk, s(t) gk, s(x)) | (Mode Expansion) |
| ∂t Ak, s(t) | = | –i Ek Ak, s(t) | |
| ∂t Bk, s(t) | = | +i Ek Bk, s(t) | (Equations of Motion) |
| LRD | = | Σk in K3, s=±½
(Ek/m) [
i (Ak, s(t)*∂t Ak, s(t)
– Bk, s(t)*∂t Bk, s(t)) – Ek (Ak, s(t)*Ak, s(t) + Bk, s(t)*Bk, s(t))] |
(Lagrangian) |
| ΠA, k, s(t) | = | i (Ek/m) Ak, s(t)* | |
| ΠB, k, s(t) | = | –i (Ek/m) Bk, s(t)* | |
| ΠA*, k, s(t) | = | 0 | |
| ΠB*, k, s(t) | = | 0 | (Momenta) |
| HRD | = | Σk in K3, s=±½ (Ek2/m) (Ak, s(t)*Ak, s(t) + Bk, s(t)*Bk, s(t)) | |
| = | –i Σk in K3, s=±½ Ek [ΠA, k, s(t) Ak, s(t) – ΠB, k, s(t) Bk, s(t)] | (Hamiltonian) | |
Although it takes a fair bit of work to derive the Lagrangian and Hamiltonian in terms of the mode coefficients Ak, s(t) and Bk, s(t), it’s not hard to verify the results, by checking that they give the required equations of motion from the Euler-Lagrange and Hamilton’s equations respectively.
To turn the classical Hamiltonian into an operator on a Hilbert space of quantum states of the field, we will need to modify the procedure we used when quantising the harmonic oscillator and the scalar field modes. There, we found that the commutators between the creation and annihilation operators were given by:
[aα, aβ†] = δα, β
[aα, aβ] = 0
[aα†, aβ†] = 0
where α and β label the mode. But because the Dirac field describes fermions, we want the states we get by applying creation operators to the vacuum state ψ0 to be antisymmetric in the mode labels:
aα† aβ† ψ0 = – aβ† aα† ψ0
This can be achieved if we replace one of the commutators with an anticommutator:
{aα†, aβ†} = aα† aβ† + aβ† aα† = 0
Taking the Hermitian conjugate of that gives us:
{aα, aβ} = 0
Following Zee[8], we can also justify a third anticommutator:
{aα, aβ†} = δα, β
by requiring that the number operator, N = Σα aα† aα, satisfies:
N aβ† = aβ† N + aβ†
This is a reasonable requirement, because applied to a state ψn with n quanta – none of which are yet in the mode β, so that aβ† ψn = ψn+1 – it becomes:
N aβ† ψn = aβ† N ψn + aβ† ψn
N ψn+1 = (n+1) ψn+1
Given the proposed anticommutator, along with the earlier claim that all creation operators should anti-commute, we can derive the required identity:
N aβ† = Σα aα† aα aβ†
= Σα aα† (δα, β – aβ† aα)
= aβ† – Σα aα† aβ† aα
= aβ† + aβ† Σα aα† aα
= aβ† N + aβ†
Now, the classical Hamiltonian we’ve found:
HRD = –i Σk in K3, s=±½ Ek [ΠA, k, s(t) Ak, s(t) – ΠB, k, s(t) Bk, s(t)]
is in a form that would make perfect sense if we identified these coordinates and momenta more or less directly with annihilation and creation operators for each mode:
Ak, s(t) → √[m/Ek] ak, s
Bk, s(t) → √[m/Ek] bk, s†
ΠA, k, s = i (Ek/m) Ak, s(t)* → i √[Ek/m] ak, s†
ΠB, k, s = –i (Ek/m) Bk, s(t)* → –i √[Ek/m] bk, s
One question that arises, though, is whether we’re entitled simply to choose the order of products of the coordinates and momenta any way we like, when we convert them to operators. It would be slightly less ad hoc to do something symmetrical that includes both ways of ordering these non-commuting operators – or, since the field is fermionic, something antisymmetrical. So we will apply the rules:
ΠA, k, s(t) Ak → [i/2] (ak, s† ak, s – ak, s ak, s†) = i (ak, s† ak, s – ½)
ΠB, k, s(t) Bk → [–i/2] (bk, s† bk, s – bk, s bk, s†) = –i (bk, s† bk, s – ½)
Putting everything together, we end up with:
| Quantised Riemannian Dirac Field | |||
| HRD | = | Σk in K3, s=±½ Ek [ak, s† ak, s + bk, s† bk, s – 1] | (Hamiltonian) |
Admittedly, what we’ve done here is very far from rigorous! Nevertheless, the Hamiltonian operator we’ve arrived at certainly attributes the correct energy, Ek, to each quantum added to the field.
If we take the result seriously, the energy of the vacuum state (for this field alone) will be negative:
HRD ψ0 = E0 ψ0
E0 = – Σk in K3, s=±½ Ek
≈ – 4 Nmodes m / (3 π)
Here Nmodes is the number of scalar modes consistent with the particle mass and the geometry of the universe, and we’ve included a doubling in the other factors to account for the two spins.
A negative vacuum energy for fermions isn’t peculiar to Riemannian physics; the same thing happens in Lorentzian QFT. As with the scalar field, the difference in the Riemannian case is that we have a finite number of modes, so the vacuum energy is finite.
[1] An Introduction to Quantum Field Theory by Michael E. Peskin and Daniel V. Schroeder, Westview Press, 1995. Section 3.2.
[2] For example, Quantum Mechanics by Leonard I. Schiff, McGraw-Hill, 1968. Section 13 derives the harmonic oscillator wave functions, while section 25 uses the ladder operator approach.
[3] Peskin and Schroeder, op. cit., chapter 2.
[4] The Quantum Theory of Fields, Volume I: Foundations by Steven Weinberg, Cambridge University Press, 1995. Sections 1.2, 5.2.
[5] Mechanics by L.D. Landau and E.M. Lifshitz, Butterworth-Heinemann, 1976. Section 45. N.B.: the Poisson bracket defined by Landau and Lifshitz in their eqn (42.5) is the opposite of the convention we’re using.
[6] Quantum Mechanics and Path Integrals by Richard P. Feynman, Albert R. Hibbs and Daniel F. Styer, Dover, 2010.
[7] Spinors and Trialities by John Baez.
[8] Quantum Field Theory in a Nutshell by A. Zee, Princeton University Press, 2010. Chapter II.2
|
|
|