

The full, general-relativistic calculations for the geodesics that photons follow when they skim past a black hole, possibly orbiting it several times before escaping, are quite involved. I described the details (for a non-rotating Schwarzschild black hole) here.
But if you’re looking at a black hole from a great distance, the optical effects become much simpler to describe. When a ray of light approaches a black hole with an impact parameter (the distance of its asymptotic straight-line path from the centre of the hole) of b, the angle by which it is deflected is given by:
δ ≈ 2 Rs/b
where Rs is the Schwarzschild radius. We also have:
b ≈ θ d
where d is the distance from an observer to the black hole and θ is the angle between the direction in which they see the light ray arriving, and the direction of the centre of the black hole. This means the true direction of the source of the light lies at an angle:
α = θ – 2 Rs / (θ d)
If we want to reverse the calculation and find the apparent angle, θ, from the true angle, α, that amounts to solving a quadratic, and we get:
θ = (1/2)(α ± √(α2 + 8 Rs/d))
One of these roots is always negative and one is always positive, because they describe the two paths that light can take, passing on either side of the black hole. When α=0, the two roots have the same size, θ = ±√(2Rs/d), which is the nominal radius of a perfect Einstein ring, created by an infinitesimally small light source that lies precisely behind the black hole.
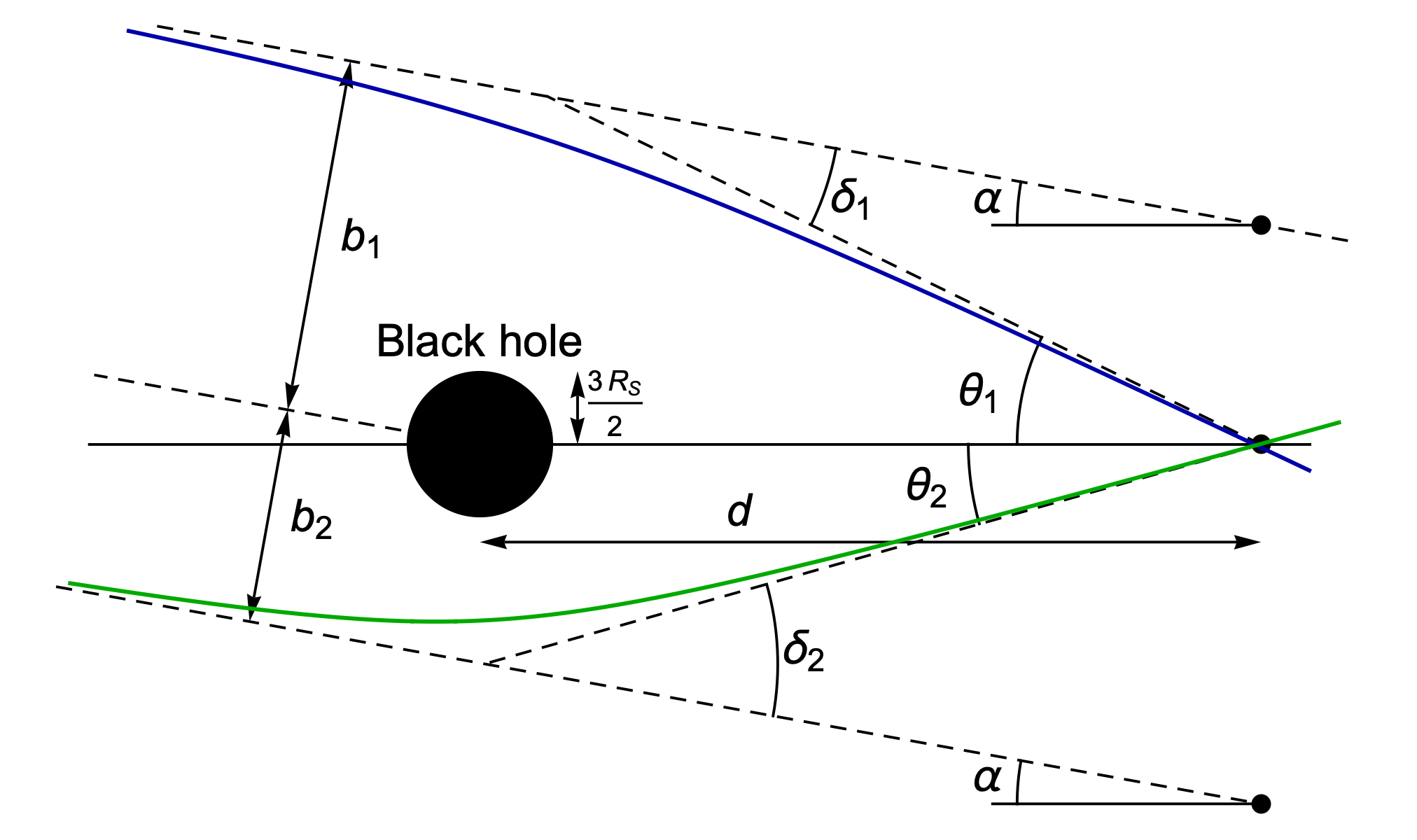
Note that the black hole itself will cover a much smaller angle in the sky than the typical angles at which gravitational lensing effects become visible. Light only falls into the black hole if it passes closer than (3/2)Rs, which the exact calculations show occurs when b ≤ (3(√3)/2)Rs. If d >> Rs then the angular radius of that “shadow”, (3(√3)/2)Rs/d, is much smaller than the radius of the Einstein ring, √(2Rs/d).
Of course real light sources aren’t points, they’re small disks, so we should ask what happens when we apply this two-valued function from α to θ to a small disk in the sky, offset by some angle from the centre of the black hole.
If the disk of the star lies far from the black hole, we will have α >> Rs/d for the whole disk, and so the two roots will just be θ ≈ α and θ ≈ 0. The first root will give an almost undistorted image of the star, while the second will produce a very small image much closer to the hole.
But as the star comes closer to the hole, the image from the positive root [the blue outline, in the image below] will begin to shift away from the hole [compared to its un-lensed location, the black outline] and grow distorted, while the image from the negative root [the green outline] will move away from the hole, and start to grow much larger. Both will stretch out into annular arcs, and if the centre of the black hole ends up within the disk of the original image of the star, the two arcs will merge and form a complete ring.

One cool thing is that, even when the black hole is so distant that it is impossible to resolve any of these geometric effects – that is, the Einstein rings (or arcs) are too small to see in any telescope – the magnification of the star’s image can still be detected simply by the resulting increase in brightness. If you observe millions of stars for long enough, you can see a characteristic peak in the plot of brightness over time for some of them, which indicates that a massive object (not necessarily a black hole) has passed in front of them. This kind of thing is used to put statistical limits on the proportions of dark matter that might be explained by various kinds of massive, compact objects rather than exotic new elementary particles.
There is a fairly simple formula for the factor by which the brightness of a star increases, in the limit that its apparent disk is small, in terms of a quantity u that is defined as:
u = α / RE
where α is the true angle for the star (measured from the direction of the centre of the black hole), and RE = √(2Rs/d) is the angular radius of the Einstein ring. In terms of u, we then have the equivalent ratio for the two apparent angles:
θ / RE = (1/2)(u ± √(u2 + 4))
Now, if we have a patch of the sky in spherical polar coordinates, the pole in the direction of the black hole, with angles α to α+dα measured from the hole and azimuthal angles φ to φ+dφ around the hole, the lensing effects will leave φ and dφ unchanged, but replace α and dα with θ and dθ. So the ratio of solid angles is:
Ω/Ω0 = (sin(θ) dφ) / (sin(α) dφ) (dθ/dα) ≈ (θ/α) (dθ/dα)
For one of the solutions, this ratio is negative, but if we add the absolute values of both ratios, we get the total:
Ω/Ω0 = (u2+2) / [u √(u2+4)]
We derived this expression by looking at the ratio of solid angles for a portion of the sky after the effects of gravitational lensing, but the same formula also tells us L/L0, the ratio by which the total brightness of the star is changed. A bundle of rays travelling from the star to the observer must shrink by exactly the same factor as an imaginary bundle of rays traced backwards from the observer’s eye to see how much sky fits into their unit solid angle of view, so the number of photons arriving at the observer per unit area is proportionately increased.
|
|
|