

The aim of this page is to assemble a variety of simple proofs for the wonderful fact, first proved by Isaac Newton, that the orbits of bodies subject to an inverse-square force are conic sections: ellipses, circles, parabolas, hyperbolas or straight lines.
Although conic sections are defined in the first instance as the curves produced when a plane intersects a cone, these curves have a wealth of well-known properties that characterise them equally well. The idea of this page is to explore the relationship between the inverse-square force law and as many of these properties as possible.
Further reading:

If you stand at one focus of a room with elliptical walls, any sound waves that leave you in a horizontal direction and bounce off the walls will be reflected along paths that take them through the other focus of the ellipse. This is a characteristic property of the geometry of ellipses: if you draw a line from one focus out to the curve, and reflect it as if in a mirror tangent to the curve, the reflected ray will pass through the other focus.
Our aim will be to show that the path of a body moving under an inverse-square force has that “whispering gallery” property. Later, we’ll describe the slightly modified forms this property takes for parabolas and hyperbolas.

In the case of an orbit, a tangent to the curve is given by the velocity vector v, while a vector perpendicular to our imaginary mirror is Rv, where R rotates vectors counter-clockwise by 90 degrees.
The law of reflection for a vector x in a mirror with a unit-length normal n is:
x → x – 2 (x · n) n
so if we reflect the vector r in the mirror whose unit-length normal is Rv/v we get:
r → r – 2 (r · Rv/v) Rv/v
We can multiply this reflected vector by v2 to get a more convenient vector to work with, still pointing in the same direction:
s = v2 r – 2 (r · Rv) Rv
= v2 r + 2 L Rv
Here we’ve made use of the fact that the dot product r · Rv is just the opposite of the angular momentum per unit mass, L. By construction, |s| = v2 r. The rate of change of s is:
ds/dt = 2 (v · a) r + v2 v + 2 L Ra
= –(2 k/r3)[(v · r) r + L Rr] + v2 v
It turns out that ds/dt is parallel to v. We can show this by taking its dot product with the vector Rv, which is orthogonal to v:
Rv · (ds/dt) = –(2 k/r3) [(v · r) (Rv · r) + L (Rv · Rr)]
= –(2 k/r3) [(v · r) (–L) + L (v · r)]
= 0
To determine the factor by which v must be multiplied to give us ds/dt, we take the dot product of the two:
v · (ds/dt) = –(2 k/r3) [(v · r)2 + L2] + v4
= –(2 k/r3) [v2 r2] + v4
= v2 (v2 – 2 k/r)
= 2 v2 E

The simplification of the expression in square brackets between the first and second lines comes from noting that L = –Rv · r, which means that the two terms here are the squares of the coordinates of r in an orthonormal basis {v/v, – Rv/v}, multiplied by v2. Hence their sum is the squared length of r, multiplied by v2.
It follows that:
ds/dt = 2 E v
So not only is ds/dt always parallel to v (which will be true for any central force), it’s equal to a constant multiple of v. That’s only true for the inverse-square law.
Making use of this relationship, we can now construct a constant vector z:
z = r – s / (2 E)
dz/dt = dr/dt – (ds/dt) / (2 E)
= v – v
= 0
This tells us that by travelling the right distance along the reflected ray, we will always pass through the same fixed point: if the centre of attraction lies at the origin of our coordinates, that point is z.
So we’ve established the “whispering gallery” property for the orbit: rays from one focus, at the centre of attraction, will all be reflected so that they pass through the second focus at z.
The vector z is almost the same as a famous conserved vector known as the Laplace-Runge-Lenz vector, but although the Laplace-Runge-Lenz vector points along the axis of the ellipse, it’s not usually defined as the displacement vector from one focus to the other. For ease of comparison, we can rewrite z as follows:
Rv = n × v, where n is a unit normal to the plane of the orbit, and × is the vector cross product
L Rv = L × v, where L is the orbiting body’s angular momentum vector divided by its mass
s = v2 r + 2 L × v
z = r – (v2 r + 2 L × v) / (2 E)
= (2 E r – v2 r – 2 L × v) / (2 E)
= (2 (½v2 – k/r) r – v2 r – 2 L × v) / (2 E)
= (v × L – k (r/r) ) / E
The exact definition of the Laplace-Runge-Lenz vector varies from author to author, and in any comparisons we need to keep in mind that our L and E are per unit mass, and our k is a constant that yields acceleration (as opposed to force) when divided by r squared. But in any case, the LRL vector is usually not divided by energy, as z is, and what most authors differ on are overall factors of the orbiting body’s mass.
For elliptical (and circular) orbits, the energy E is negative. What happens if E is zero? In that case we can’t construct the vector z, but since ds/dt = 0 the reflected vector s will now always point in the same direction. This is the characteristic property of a parabola, which reflects rays from its single focus so that they all end up parallel.
If E is positive, z lies on the opposite side of the trajectory from the centre of attraction. The orbit becomes a hyperbola, with the reflected rays diverging away from a virtual focus.
 |
 |
 |
| E < 0, elliptical orbit | E > 0, hyperbolic orbit | E = 0, parabolic orbit |
| Any ray from either focus will be reflected so that it passes through the other. | Any ray from either focus will be reflected so that it seems to come from the other. | All rays from the focus will be reflected in a common direction. |
To draw an ellipse, place a sheet of paper on a cork board and insert two pins where you’d like the two foci of the ellipse to be. Take a loop of string and encircle the pins with it, then insert the tip of a pencil in the loop and make the string taut, so it forms a triangle. As you drag the tip of the pencil around in a closed curve, the sum of the distances of its tip from the two foci will remain constant. This is probably the best-known definition of an ellipse – and it generalises to the other conic sections.
 |
 |
 |
| E < 0, elliptical orbit | E > 0, hyperbolic orbit | E = 0, parabolic orbit |
| The sum of the distances from the two foci remains constant. | The difference between the distances from the two foci remains constant. | The distance from the focus is equal to the distance from the directrix. |
We can adapt the proof from the previous section to show that our inverse-square-law orbits also have the “pins, string and pencil” property. The distance of the orbiting body from the centre of attraction is simply r. But what is the distance of the body from the fixed point z? We started by reflecting the vector r, producing a new vector of the same length, r, but then we multiplied that reflected vector by v2 to get s. So |s| = v2 r. But to reach z from the orbiting body, we used s / (–2 E). So the orbiting body is at a distance of v2 r/(|2 E|) from z. So long as E < 0, this gives us:
Sum of distances from the two foci
= r + v2 r/(–2 E)
= r (1 – v2 /(2 E))
= r (2 E – v2)/(2 E)
= r ((v2 – 2 k/r) – v2)/(2 E)
= –k / E
This is constant, and since E is negative it will be a positive quantity.
You can’t draw a hyperbola with the same method, but the algebra goes through identically to show that the difference between the distances from the two foci is constant, with its absolute value equal to k / E for positive E.
The related definition of a parabola is that it’s the curve equidistant from a point, the focus, and a straight line known as the directrix that lies perpendicular to the axis of symmetry. The vector s, which is constant for a parabola, will be parallel to that axis.
We can find the axial component of the distance of the orbiting body from the focus by taking the dot product of r with a unit vector parallel to the axis: s/|s| = s/(v2 r).
Axial component of distance from focus
= r · s/(v2 r)
= r · (v2 r + 2 L Rv) / (v2 r)
= (v2 r2 + 2 L (r · Rv)) / (v2 r)
= (v2 r2 – 2 L2) / (v2 r)
= r – 2 L2 / (v2 r)
Since the energy is zero, we have:
2 E = v2 – 2 k/r = 0
v2 r = 2 k
Applying this to the previous result we have:
Axial component of distance from focus = r – L2 / k
So if we place the directrix L2 / k away from the focus in the opposite direction to s, we will have:
Perpendicular distance from directrix
= L2 / k + Axial component of distance from focus
= r
This shows that our orbit for E = 0 fulfills the definition of a parabola.
In the previous section we described the parabola as the curve that’s equidistant from a point, the focus, and a line, the directrix. But it turns out that we can generalise this to describe the other conic sections in a very similar way. We simply require that instead of being equal, the distance from the focus and the distance from the directrix maintain a fixed ratio, known as the eccentricity, ε.
 |
 |
 |
| ε < 1, elliptical orbit | ε > 1, hyperbolic orbit | ε = 1, parabolic orbit |
| The distance from the focus divided by the distance from the directrix is a constant, less than 1. | The distance from the focus divided by the distance from the directrix is a constant, greater than 1. | The distance from the focus is equal to the distance from the directrix. |
The circle can only be constructed this way as a limiting case, where the eccentricity ε approaches zero while the distance to the directrix goes to infinity, with the product of the two held constant at the radius of the circle.

Although we’ve already proved the desired relationship for the parabola, we’ll now show that this constant ratio of distances holds for all the orbits produced by the inverse-square law.
We’ll adopt coordinates as shown in the image on the right, with the origin at the focus and the directrix having an x-coordinate of –D. The distance from the directrix to some point (x, y) on the curve is then simply x+D.
The defining relationship of the conic section is:
r = ε (x + D)
It follows that:
x = r / ε – D
cos θ = x / r = 1 / ε – D / r
Differentiating, we get:
–sin θ dθ = (D / r2) dr
dr/dθ = –sin θ (r2 / D) = –y r / D
(dr/dθ)2 = (r / D)2 y2
= (r / D)2 (r2 – x2)
= (r / D)2 (r2 – (r / ε – D)2)
The last equation can be rewritten as:
(dr/dθ)2 = (1 – 1/ε2) r4 / D2 + 2 r3 / (D ε) – r2
Now, what we wish to show is that the inverse-square force results in a relationship between (dr/dθ)2 and r that takes the same form as this. We start with the basic statement of conservation of energy, and convert the squared velocity into polar coordinates:
E = ½v2 – k/r
2 E + 2 k / r = v2
= r2 (dθ/dt)2 + (dr/dt)2
= (dθ/dt)2 [r2 + (dr/dθ)2]
In the last step we’ve used the chain rule: dr/dt = (dr/dθ) (dθ/dt). From conservation of angular momentum:
dθ/dt = L / r2
Combining these, we have:
(L / r2)2 [r2 + (dr/dθ)2] = 2 E + 2 k / r
Solving for (dr/dθ)2 gives us:
(dr/dθ)2 = (2 E / L2) r4 + (2 k / L2) r3 – r2
So we’ve ended up with exactly the same form for this relationship as we obtained by fixing the focus-directrix ratio. By choosing suitable values for D and ε we can make the two equations identical.
If we reverse the direction of our argument and assume that a body’s path through space is a conic section, and that its motion is due to some kind of central force with a centre of attraction at one focus of the conic, we can prove very easily that the force must follow the inverse-square law. The one exception to this is if the conic section is a perfect circle; any attractive force will admit circular orbits around the centre of attraction.

In the diagram on the right, we’ve assumed the orbit is an ellipse, and so the sum of the distances to the two foci is equal to some constant, B, while Rv, being perpendicular to the curve, bisects the angle subtended by the two foci.
By conservation of energy with a central-force potential U(r):
E = ½v2 + U(r)
v2 = 2 (E – U(r))
By the definition of angular momentum, we have:
L = v r sin β = v r cos α
L2 = v2 r2 cos2 α = 2 r2 (E – U(r)) cos2 α
Using the cosine law for triangles and a basic trigonometric identity, we have:
cos 2α = (r2 + (B – r)2 – C2) / (2 r (B – r))
cos2 α = ½ (1 + cos 2α) = ½ (B2 – C2) / (2 r (B – r))
L2 = ½ (B2 – C2) (E – U(r)) / (–1 + B/r)
But we know that L2 is a constant, independent of r, and this can only be true if E – U(r) is some constant multiple of –1 + B/r, allowing the dependence on r to cancel out. That means U(r) must be inversely proportional to r, giving an inverse-square force law.
Very similar arguments can be made for the hyperbola and the parabola.
Note that cos2 α, which measures the extent to which the tangent to the orbit deviates from a purely circular direction, can also be expressed in the intuitively appealing form:
cos2 α = r+ r– / (r (r+ + r– – r))
where r+ = ½ (B + C) is the aphelion distance and r– = ½ (B – C) is the perihelion distance. This is clearly equal to 1 when r = r±.
How does this change if we place the centre of attraction at the centre of the ellipse, rather than at a focus? We then have:
cos2 α = a2 b2 / (r2 (a2 + b2 – r2))
where a and b are the semi-axes of the ellipse. This is clearly 1 when r = a or b. With this new assumption about the centre of attraction, the expression for L2 becomes:
L2 = 2 a2 b2 (E – U(r)) / (a2 + b2 – r2)
In order for L2 to be constant in this case, E – U(r) must equal a constant multiple of a2 + b2 – r2, meaning U(r) must be proportional to r2. This describes a two-dimensional harmonic oscillator potential.
Imagine an ellipse centred on the origin in the complex plane, with its major axis lying on the x-axis. Suppose we “square” every point of this ellipse, using the rules of complex arithmetic:
(x + y i)2 = (x2 – y2) + 2 x y i
What does the new curve, consisting of the squared points, look like?
If our ellipse has semi-axes a and b, any point on it can be written in the form:
(x, y) = (a cos φ, b sin φ)
where we should stress that φ is just a parameter along the curve, not the polar angle of this complex number. We’ll define the coordinates of our squared points as X = x2 – y2 and Y = 2 x y. We then have:
(X, Y) = (a2 cos2 φ – b2 sin2 φ, 2 a b sin φ cos φ)
= (½(a2 – b2) + ½(a2 + b2) cos 2φ, a b sin 2φ)
This describes an ellipse centred at (½(a2 – b2), 0), with semi-axes of ½(a2 + b2) along the X-axis and ab along the Y-axis.
Where are the foci of this new ellipse? By symmetry they will lie at (½(a2 – b2) ± c, 0), for some quantity c. The sum of the distances of any point on the ellipse from the two foci must be equal to the full length of the major axis: a2 + b2. Since the vertical semi-axis is ab, the point on the top of the ellipse is (½(a2 – b2), ab), and its distance from each focus is √(c2 + a2 b2). So we have:
c2 + a2 b2 = [½(a2 + b2)]2
c = ½(a2 – b2)
That means the two foci are (0,0) and (a2 – b2, 0). One focus is the origin!
Squaring every point of an ellipse centred on the origin of the complex plane yields a new ellipse whose focus lies at the origin.
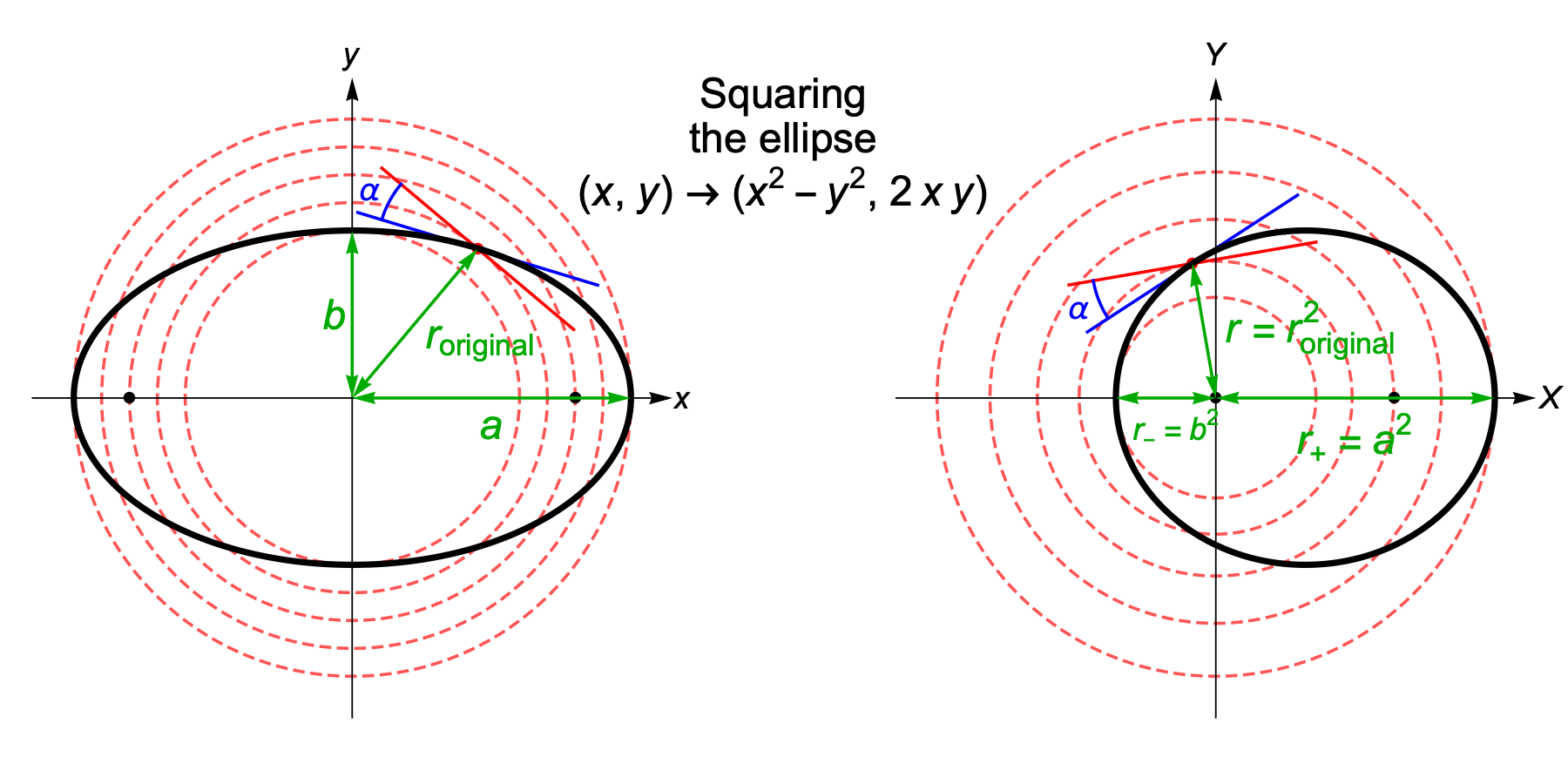
What’s more, squaring a complex number is a conformal map: it leaves the angles between curves unchanged. So the angle beween the original ellipse and a circle of radius r at the point where they intersect (such as α in the diagram above) will be exactly the same as the angle between the new ellipse and a circle of radius r2. (To be precise, squaring is a conformal map on the complex plane excluding the origin. So the right angle between the real and imaginary axes where they meet at the origin is not preserved by the map.)
Now, consider a particle that’s free to move in two dimensions, subject to an attractive force that’s a constant multiple of its distance from a centre of attraction. A system like this is known as a two-dimensional harmonic oscillator. If we choose coordinates whose origin lies at the centre of attraction, the particle’s acceleration will take the form:
d2r(t)/dt2 = –ω2 r(t)
where ω is related to the force constant and the particle’s mass. In Cartesian coordinates, the particle’s x and y coordinates will both oscillate with the frequency ω, while being free to take on arbitrary amplitudes and phases:
x(t) = C sin(ω t + φ)
y(t) = D sin(ω t + ψ)
It’s easy to check that this satisfies our equation for the acceleration. By a suitable rotation of the coordinates and choice of origin for t, we can always put this trajectory into the form:
x(t) = a cos(ω t)
y(t) = b sin(ω t)
with a ≥ b. Clearly this traces out an ellipse with semi-axes a and b, centred on the origin, with the major axis lying on the x-axis.
The acceleration equation corresponds to the harmonic oscillator potential (given here as potential energy per unit mass):
USHO(r) = ½ ω2 r2
At the end of the previous section, we claimed without proof that the squared cosine of the angle α for an ellipse centred on the origin was:
cos2 α = a2 b2 / (r2 (a2 + b2 – r2))
But since we’ve now established independently that USHO gives rise to elliptical orbits centred on the origin, we can derive cos2 α from its relationship with the angular momentum:
L2 = v2 r2 cos2 α = 2 r2 (E – USHO(r)) cos2 α
cos2 α = L2 / [2 r2 (E – ½ ω2 r2)]
Consider the particle at t=0, when it lies at the point (a, 0). Taking the derivative of the trajectory, its velocity is (0, ωb). Its potential energy (per unit mass) will be ½ω2 a2, its kinetic energy (per unit mass) will be ½ ω2 b2, and its angular momentum (per unit mass) will be L = ωab. So the equation above gives us the result we claimed:
cos2 α = ω2 a2 b2 / [2 r2 ½ω2 (a2 + b2 – r2)] = a2 b2 / (r2 (a2 + b2 – r2))
Because squaring is a conformal map that preserves angles, the formula for cos2 α for a “squared” ellipse whose focus lies on the origin must take the same form, with r2 replaced by r and a2 and b2 replaced by the aphelion and perihelion distances r±:
cos2 α = r+ r– / (r (r+ + r– – r))
In order for the angular momentum to be constant for a body moving around this new ellipse, we’re led again to a potential that’s inversely proportional to r, and an inverse-square force law.
L2 = v2 r2 cos2 α = 2 r2 (E – U(r)) r+ r– / (r (r+ + r– – r))
E – U(r) = [L2 / (2 r+ r–)] [–1 + (r+ + r–) / r ]
The connection between the two kinds of force laws can be made in much more detail than this, and in fact it’s possible to map trajectories for a particle in the harmonic oscillator moment-by-moment into trajectories for the inverse square law, by means of a suitable re-scaling of the time coordinate[1][2].
No discussion of conic sections would be complete without exhibiting an actual cone. We will do so with the aid of a beautiful construction known as the Dandelin spheres.

Pick two points F1 and F2 in a plane whose normal vector is n. Place a sphere of radius ρ1 on one side of the plane, tangent to it at F1, and a sphere of radius ρ2 on the other side of the plane, tangent to it at F2. (In the view on the right, the plane is seen edge-on.)
Now construct a cone so that both spheres sit inside it, tangent to its sides. The intersection of this cone and our chosen plane will be an ellipse with foci F1 and F2.
If the distance between the foci is 2 c, the semi-major axis of the ellipse will be a = √(c2 + ρ1 ρ2) and the semi-minor axis will be b = √(ρ1 ρ2). The geometry of the ellipse itself doesn’t fix a unique pair of Dandelin spheres, or a unique cone. One simple choice would be to set ρ1 = r–, the perihelion distance, and ρ2 = r+, the aphelion distance, but in what follows we won’t rely on any particular choice.
By definition, the intersection of a cone and a plane that forms a simple closed curve like this is an ellipse, but we can use this construction to prove some of the properties of the ellipse that we assumed in previous sections. Dandelin spheres can also be used to establish the analogous properties of hyperbolas and parabolas.
 |
To prove that the sum of the distances from the two foci to any point P on the ellipse is constant, consider the diagram on the left. The points P1 and P2 are found by passing a line through P to the tip of the cone, S, and intersecting it with the circles where the two spheres are tangent to the cone. The planes in which those circles lie are both orthogonal to the axis of the cone, so the total distance P1P2 is clearly constant, independent of P.
But the distance PF1 is equal to the distance PP1, since both these line segments are tangents from the same point, P, to the same sphere. Similarly, the distance PF2 is equal to the distance PP2. So PF1 + PF2 = PP1 + PP2 = P1P2, a constant.
The planes through the circles where the two spheres are tangent to the cone intersect the original plane along two lines; these lines are the directrices of the ellipse, D1 and D2. We will project our generic point P on the ellipse to points Q1 and Q2 on the directrices.
The ratio between the distance of a point P on the ellipse to one focus, PF1, and the distance to the corresponding directrix, PQ1, is the same as the ratio PP1 to PQ1. Now, the line segments P1Q1 and P2Q2 are parallel, since they lie in the intersections of two parallel planes with the plane that contains all four endpoints. This means the triangle P1PQ1 is similar to the triangle P2PQ2.
It follows that:
PP1 / PQ1 = PP2 / PQ2
But we also have two constant sums of distances:
PP1 + PP2 = C
PQ1 + PQ2 = D
This lets us write:
PP1 / PQ1 = (C – PP2) / (D – PQ2) = PP2 / PQ2
PQ2 (C – PP2) = PP2 (D – PQ2)
PP2 / PQ2 = C / D
And of course PP1 / PQ1 is the same. So the ratio between the distance from a point on the ellipse to one focus and the distance to the corresponding directrix is constant.

We wish to show that the angles between the tangent to the ellipse at any point P and the vectors P – F1 and P – F2 are the same. More precisely, the angle between P – F1 and a given tangent vector t must be the same as the angle between P – F2 and the opposite of that vector, –t. That will guarantee that any ray from one focus that is reflected in the normal to the curve will pass through the other focus: the “whispering gallery” property.
We previously defined P1 as the point lying on both a line from P to the tip of the cone and on the circle where the first Dandelin sphere is tangent to the cone. There are two examples in the image on the right, P1 and P1′, for two different points on the ellipse, P and P′, but the general case can be seen in the animation earlier in this section.
Any vector normal to the cone at P will be parallel to a normal at P1, and at P1 the normal to the cone coincides with the normal to the first Dandelin sphere. So we can obtain a vector normal to the cone at P simply by taking the vector from the centre of the sphere to P1:
N1 = P1 – C1 = P1 – (F1 + ρ1 n)
From this, we can construct a tangent to the ellipse that lies in the plane normal to n:
t1 = N1 × n = (P1 – F1) × n
Now, since t1 is perpendicular to P1 – F1, the dot product of any vector with t1 will be unchanged if we add or subtract some multiple of P1 – F1 to the original vector. So the dot product of t1 with the vector from the first focus to P is:
(P – F1) · t1 = (P – F1 – (P1 – F1)) · t1 = (P – P1) · t1
We can now calculate the cosine of the angle between the vector from the first focus and the tangent:
cos β1 = (P – F1) · t1 / [|P – F1| |t1|]
= (P – P1) · t1 / [|P – F1| |t1|]
= p1 · t1 / |t1|
= p1 · t0
We’ve made use of the fact (shown earlier) that |P – F1| = |P – P1|, and we’ve defined p1 = (P – P1) / |P – P1| as the unit vector that points from P1 to P. We’ve also defined t0 = t1 / |t1| as the normalised tangent vector.
We can repeat this entire construction with the roles of the foci swapped, defining a normal N2 parallel to N1, and a tangent t2 parallel to t1. Because t1 and t2 are parallel (rather than antiparallel), we end up with exactly the same normalised tangent vector, t0. We conclude that the angle between the vector from the second focus and the tangent t0 satisfies the equation:
cos β2 = p2 · t0
where p2 is the unit vector that points from P2 to P, and hence p2 = –p1. But if we want the angle with the opposite tangent vector, –t0, its cosine will be:
cos (π–β2) = p2 · (–t0) = p1 · t0 = cos β1
So we find exactly the same angle between the vector from the first focus and t0 as between the vector from the second focus and –t0, as expected.
 |
We can exhibit a moving square tangent to the cone whose area is inversely proportional to the kinetic energy of the orbiting body! This square’s bottom edge lies on a line that’s tangent to the ellipse, while its top corner is always the point P1 that follows the circle where the cone meets the first Dandelin sphere.
Why is the area of this square inversely proportional to the kinetic energy? As discussed in the previous subsection, the line PP1 makes the same angle with the tangent to the ellipse as the line from the focus, PF1, and the length PP1 is equal to the length PF1, i.e. the distance r of the orbiting body from the centre of attraction. So the area of the square is:
Area = r2 sin2 β
where β is the angle between the tangent and a line to the centre of attraction.
If L is the angular momentum of the orbiting body per unit mass, we have:
L = v r sin β
L2 = v2 r2 sin2 β = 2 K(r) Area
Area = ½ L2 / K(r)
where K(r) = E – U(r) is the kinetic energy of the orbiting body per unit mass.
In the section From Shape To Force Law we derived an expression for sin2 β (written there as cos2 α, for α=π/2–β) from the geometrical properties of an ellipse, and used it to show that the potential U(r) that produces elliptical orbits must be inversely proportional to r. Here we will give a slightly different argument that leads to the same conclusion.
First, we’ll define:
f(r) = sin2 β
If we write 2a for the constant sum of distances from a point on the ellipse to the two foci, it’s clear that we must have the symmetry:
f(r) = f(2a – r)
since r → 2a – r corresponds to moving a point to its reflection in the minor axis of the ellipse, changing β to π–β and leaving sin β unchanged. Now, if we define a function:
g(p) = f(a + √[a2 – p])
we have:
g(r (2a – r)) = f(a + √[(a – r)2]) = f(a ± (a – r)) = f(r)
where the choice of plus or minus makes no difference since the two alternatives lead to f(r) or f(2a – r). This proves that f can only depend on the product p = r (2a – r).

We’ll write the distances to the two foci as a ± √[a2 – p], and form a right triangle whose Pythagorean relationship is (after dividing through by 4):
a2 cos2 β + (a2 – p) sin2 β = c2
a2 – p sin2 β = c2
This gives us:
sin2 β = (a2 – c2) / p = (a2 – c2) / [r (2a – r)]
Area = r2 sin2 β = (a2 – c2) / [–1 + 2a/r]
The product of the kinetic energy K(r) = E – U(r) and the area of the square is the constant ½ L2, and that product can only be independent of r if we have a potential U(r) inversely proportional to r.
[1] Huygens and Barrow, Newton and Hooke, V. Arnol’d, Birkhäuser, Boston, 1990.
[2] “Planetary Motion and the Duality of Force Laws”, Rachel W. Hall and Krešimir Josić, SIAM Review, Volume 42, No. 1, March 2000, pp 115–124. Online as PDF.
|
|
|