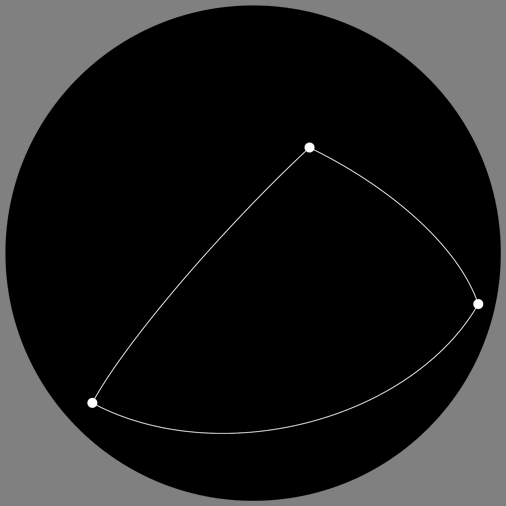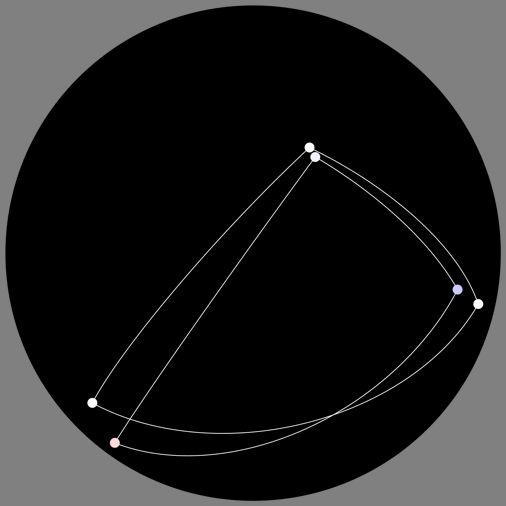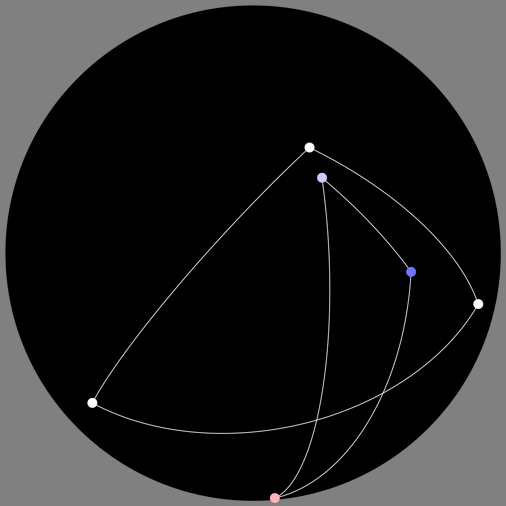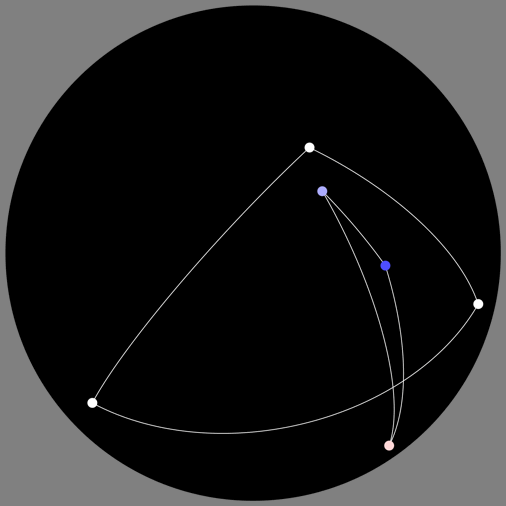
Suppose you can observe the positions in the sky of a number of stars as you undergo a continuous sequence of Lorentz transformations – boosts, rotations, or any combination thereof – but for some reason you are seeing a black-and-white image that tells you nothing about the frequency of the light you’re receiving from the stars.
This might sound like an unlikely scenario, but mathematically this is exactly what happens in a well-known model of the action of the Lorentz transformations on the appearance of the sky. The connected component of the group of Lorentz transformations containing the identity (that is, all Lorentz transformations that don’t act like reflections or reverse the direction of time) is isomorphic to the group of Möbius transformations: the fractional-linear functions on the complex plane:
z → (a z + b) / (c z + d)
with ad – bc ≠ 0.
If we stereographically project the heavenly sphere – the set of directions that light can travel in – onto the complex plane, act on the complex plane with a Möbius transformation, then project back onto the sphere, we see the stars repositioned on the sphere exactly as they would be by the corresponding Lorentz transformation.
But we don’t learn anything directly about any change in the stars’ colour due to the Lorentz transformation that corresponds to this action on the heavenly sphere.
Of course there are lots of different ways we could figure this out, but here is one solution. Suppose we keep track of the before and after shapes of the triangles formed by the same three stars; we don’t care about the stars’ absolute positions or how much they get moved across the sky, but for each pair of stars we know the angle between them, originally, and after the Lorentz transformation.
Let’s call those angles αij originally and βij after the transformation, where i,j=1,2,3.
Now, suppose the null vectors describing the energy-momentum of the light coming from the three stars are originally:
Ei (1, ai)
and after the transformation they are:
E*i (1, bi)
where we are writing these null vectors as multiples of a time component of 1 and a unit spatial vector, ai or bi.
Because the Lorentz transformation must preserve the four-dimensional dot product between pairs of these vectors, we have:
Ei Ej (1 – ai·aj) = E*i E*j (1 – bi·bj)
The (ordinary, three-dimensional) dot products ai·aj are just the cosines of the angles αij, and similarly for bi·bj and βij.
For each edge of the triangle, we define:
rij = √[(1 – cos βij)/(1 – cos αij)]
It’s then easy to solve for the ratios E*i/Ei:
E*1/E1 = r23 / (r12 r13)
E*2/E2 = r13 / (r12 r23)
E*3/E3 = r12 / (r13 r23)
which tell us how the frequency of light received from each star has changed.
So we have a kind of triangle law for Doppler shifts, revealing the value at each vertex from information about the changes in the geometry of the sides.
This also gives us an easy way to see an infinitesimal version of the law. For small angles αij and βij, we have:
rij = βij/αij
and in the limit as the angles approach zero, all ratios and Doppler shifts will approach the same value:
E* / E = α / β = the inverse of the square root of the factor by which areas change.
|
|
|