
This web page is a work in progress, giving some information and calculations relating to General Relativity in two spatial dimensions, plus time. I became interested in this subject after reading John Baez’s This Week’s Finds in Mathematical Physics, Week 232, which contains an introduction to the subject and some references.
In 2+1 dimensions, Einstein’s equation in a vacuum requires that spacetime is completely flat. This is in stark contrast to the situation in 3+1 dimensions, where the vacuum solutions are only required to be “Ricci flat”, that is, the Ricci curvature tensor must be zero, but the complete, Riemann curvature tensor need not be, allowing for gravitational waves, and for the familiar gravitational effects of the sun on the Earth, and so on.
There are 2+1 spacetimes which contain no matter at all but still exhibit non-trivial physics, because their topology is non-trivial. However, in this page I’m going to discuss another possibility, in which matter is present, and consists of individual point particles.
It turns out that the appropriate solution of Einstein’s equation for the vacuum around an ordinary point particle is for the flat spacetime to have an “angular deficit” proportional to the particle’s mass, so that the space around the particle has a total angle of less than 2π. In other words, each 2-dimensional spatial slice has the geometry of a cone. A cone can be constructed by taking a plane, cutting out a triangular wedge, and then identifying the two edges of the missing wedge. Similarly, we can construct the 2+1 spacetime containing a single particle by taking Minkowski spacetime, cutting out a solid wedge (like an infinite triangular prism) whose edge runs along the particle’s world line, and then identifying the two planes of the wedge. Assuming we use coordinates where the word line of the particle passes through the origin, there will be a Lorentz transformation that leaves the particle’s world line unchanged, but which rotates one of the planes of the wedge on to the other.
In a region of flat spacetime, the parallel transport of a tangent vector around a loop will leave the tangent vector unchanged if the loop is contractible, i.e. if it can be shrunk down to a point while remaining in the region where spacetime is flat. However, if we parallel-transport a tangent vector in a loop that goes around the particle’s world line, it will come back rotated, by the same Lorentz transformation as we used to join the planes of the missing wedge of spacetime.
A rotation can always be characterised by an angle between zero and 2π, so particle masses in this model take on a finite range of possible values. We will call the maximum possible particle mass mmax. In conventional geometrical units, where G = c = 1, the deficit angle associated with a particle of mass m is 8πm, and so mmax = 1/4.
Now, as well as ordinary particles that move slower than the speed of light, we can imagine a similar scheme for particles that move at lightspeed, or faster. These three classes of particles are known as tardyons, luxons, and tachyons. Even if we don’t accept the possibility of actual tachyons in our model, it’s worth considering for a moment what the spacetime geometry around them would be. When we parallel-transport a tangent vector in a loop around a tardyon’s world line, the tangent vector comes back rotated by a Lorentz transformation that preserves the timelike tangent vector to the world line. A similar thing should happen for luxons and tachyons, but in those cases the Lorentz transformation that preserves the lightlike or spacelike tangent vector to the luxon or tachyon’s world line will not be a rotation. For the luxon it will be a “null rotation”, and for the tachyon it will be a boost. (Here is a link to an explanation of null rotations.)
The linear map that acts on tangent vectors when they are transported around a loop is known as the holonomy of the loop. To identify this map with a specific Lorentz transformation, that is, a specific element g of the group SO(2,1), we have to choose a base point B where we start and finish the loop, and also choose a basis for the tangent space at B. If we move the base point or change the basis, then the particular g we find for a given particle’s world line will change, becoming conjugated by some other element h of SO(2,1), g→h–1gh. However, whether a Lorentz transformation is a rotation, a null rotation or a boost, and the magnitude of its effect, is preserved by conjugation.
In a spacetime containing multiple particles, the holonomies of loops that enclose the world lines of individual particles will still behave in the way we’ve described. The holonomy of a loop that encloses several particles’ world lines will then be a product of the individual holonomies.
We will sometimes refer to the holonomy of a loop that encloses a system of particles as the system’s group-valued momentum. This is a strange concept, when we’re used to momentum being a vector, but as John Baez argues it makes a lot of sense, and even allows us to frame a modified law of conservation of momentum. If we choose a base point B and a basis for its tangent space, then draw a loop from B around a whole system of particles, the flatness of spacetime allows us to push the loop into the past or future without changing the holonomy (so long as we don’t change its homotopy class, i.e. we smoothly deform it without it ever leaving the flat spacetime of the vacuum). In other words, the group-valued momentum remains constant, whatever is happening to the system internally.
The order in which the individual holonomies are multiplied depends on choosing a scheme for ordering the particles, and these issues lead to some fascinating results, including the fact that classical particles in 2+1 GR obey exotic, “anyonic” statistics! (See John Baez’s This Week’s Finds in Mathematical Physics, Week 232 for more on this.) However, if we decide that we’re only going to pay attention to the conjugacy class of the total holonomy, then it doesn’t matter how we order the product. So we can imagine various kinds of multi-particle systems, and then multiply the individual holonomies in some arbitrary order to see what the conjugacy class of the total holonomy of the system becomes.
In what follows, we will assume that all the individual particles are tardyons.
If we have N particles at rest with respect to each other, then all the individual holonomies will be rotations around the same axis, and so the total holonomy will be too. The total angle of rotation will just be the sum of the individual rotations.
If the sum of the rotations exceeds 2π, then the total holonomy will be a rotation by the sum modulo 2π. However, I’m not sure under what circumstances this is possible, because Ralph Hartley pointed out that a flat spacelike slice with the topology of R2 (excluding the particles themselves) must have a deficit angle of at most 2π. A surface with the topology of a sphere will have a deficit angle of exactly 4π, or 2π times the Euler characteristic of the surface; the sphere has the highest Euler characteristic possible, which seems to put an upper limit on the static case. One sneaky way around this limit would be to allow particles to have “negative mass”, i.e. negative angular deficits, as well as positive ones. Then it would be possible for a group of positive-mass particles to have a collective angular deficit exceeding 2π, without the angular deficit for the entire spacelike slice crossing that threshold.
What happens if we have a system of two particles that are not at rest with respect to each other? If we let v be the speed of both particles in their centre-of-mass frame, then as v increases the total holonomy will be a rotation by ever increasing amounts, in much the same way as, in special relativity, the total energy of the same system will grow as the particles gain kinetic energy. However, once the rotation reaches 2π, it does not simply “reset to zero” and then continue as before. Instead, the total holonomy becomes a boost: the same kind of holonomy we’d get from an individual tachyon! So, even if we forbid tachyons in our model, the total group-valued momentum of a pair of particles will be tachyonic if their relative motion is high enough.
In the plot below, the tachyonic mass of the system is shown in red.

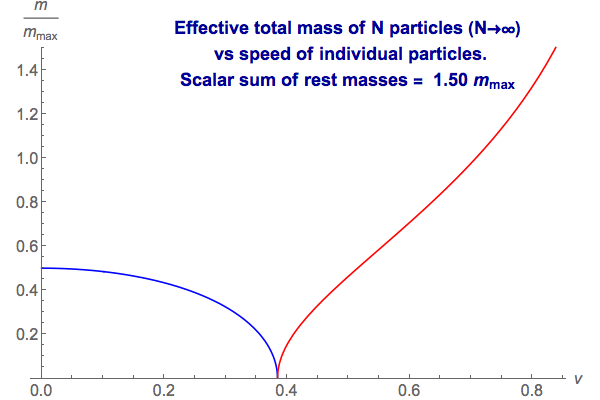
What about systems with a large number of particles? One simple kind of system to analyse is one where we have N identical particles, all moving at the same speed, v, in their centre-of-mass frame, and with their ordinary velocities arranged symmetrically, forming an N-pointed star.

It turns out that, for large N, the total holonomy of such systems depends on v and on the scalar sum of the particles’ rest mass, M. In other words, if we have N individual particles each of rest mass M/N and speed v, then as N gets larger the total holonomy converges on a fixed function of M and v.
For small values of M, the total holonomy behaves much like that of a two-particle system: as v increases it resembles a single tardyon of steadily increasing mass, and when it reaches the maximum mass, it becomes tachyonic.

For larger values of M, the behaviour of the total holonomy with increasing v becomes cyclic before becoming tachyonic. If M exceeds mmax, as v increases from zero the total group-valued momentum of the system is equivalent to that of a single particle that is growing less massive.


If two particles collide to form a third particle, we can compute the total holonomy around the two incoming particles, and then use the conservation of group-valued momentum to realise that a loop around the third, outgoing particle will have the same holonomy (though we have to be careful to base all these loops at the same point in spacetime, B, and to use some fixed basis for the tangent space at B to view the holonomy as a specific group element). We can then analyse the total holonomy to determine the conventional, vector-valued momentum of the outgoing particle. This vector result will be dependent both on the choice of basis for the tangent space at B, and the homotopy classes of the paths we use to parallel transport tangent vectors from the particle world lines to B.
With all these provisos, we can go ahead and calculate the results for the simplest case. Suppose two tardyons of equal rest mass, m, collide and form a single outgoing particle. Suppose we choose a base point B, a tangent space there, and homotopy classes of paths for parallel transport such that the incoming particles have vector-valued momenta corresponding to ordinary velocities of vex and –vex. Then it turns out that the rest mass M and ordinary velocity w of the outgoing particle will be given by:
cos(πM/mmax) = (cos(2πm/mmax) – v2) / (1 – v2)
w = –v/√(1–v2) tan(πm/mmax) ey
This result means that if an observer at B faces the site of the collision, and the particles come in from her left and right, then the outgoing particle will be moving directly towards her. This seems like a puzzling violation of the symmetry of the situation. However, if we place another observer on the opposite side of the “plane” of the collision, also facing towards it, he will also see the outgoing particle approaching. So rather than an asymmetry, we now seem to have a paradox: the outgoing particle is seen to be approaching two different observers on opposite sides!
The apparent paradox is resolved if we construct the whole spacetime for the collision. Just as we can carve triangular-prismatic wedges out of Minkowski spacetime along the world lines of individual particles, there turns out to be a remarkably simple construction for the spacetime of a “trivalent” collision. We simply take the three worldlines in Minkowski spacetime, take the interior of the “infinite tetrahedron” they define, and then glue it face-by-face to a mirror image of itself.
We can’t draw the result with all three pairs of faces glued together, but if we glue together just the faces defined by the pair of incoming world lines, we get a picture which shows wedges excised along those world lines, but with two copies of the outgoing world line.

In this picture, the two heavy lines coming in from the bottom are the incoming particles, and the two heavy lines that emerge from the collision both represent the single outgoing particle. If the two red planes are glued together, and the two blue planes are glued together, then there will be a single world line for the outgoing particle. The two dashed lines are the geodesic world lines for observers on either side of the collision who judge the incoming particles to be approaching purely from the left and right, and who both see the outgoing particle as approaching them. We can see here that they are both right, and that they end up colliding with the particle, and with each other.
This picture also gives us a useful new way to think about the Lorentz transformations that preserve the worldlines of the particles involved. In three spatial dimensions, it’s well known that any rotation about a given axis can be factored into a pair of reflections in two planes that intersect along that axis. This factoring is not unique, and as long as the angle between the planes is half that of the angle of rotation, the product of the reflections (in the correct order) will equal the rotation.
We can do something similar with Lorentz transformations in 2+1 Minkowski spacetime, but we need to be a bit careful because there are some differences and some interesting exceptions. Suppose that we have two linearly independent vectors u1 and u2 in Minkowski spacetime. Then these vectors will span a plane, and in most cases we will be able to define a reflection in that plane, ref(u1, u2), i.e. an element of O(2,1) with the following properties:
To construct ref(u1, u2) we first find a vector n12 that is normal to both u1 and u2. In three-dimensional Euclidean space this can be done with the vector cross product, and there is a Lorentzian equivalent to this:
n12a = gabεbcdu1cu2d
where we are summing over repeated indices, g is the flat metric with Lorentzian signature, and εbcd is 1 if {b,c,d} is an even permutation of {0,1,2}, –1 if it is an odd permutation, and 0 otherwise. We could also define this Lorentzian cross product in terms of the Hodge dual and the wedge product. However, in practical terms for the purpose of calculations, the most useful way to think of this formula is that if we’re using coordinates in an orthonormal basis, we can just take the ordinary Euclidean cross product, and then reverse the sign of the time coordinate (by convention, usually the first coordinate).
Having found n12, the reflection in the plane then consists of projecting vectors into the 1-dimensional subspace generated by n12 and subtracting twice this projection from the original vector, reversing the component normal to the plane:
ref(u1, u2)(w) = w – 2 (n12·w) n12 / (n12·n12)
However, if n12 is a null vector then this formula won’t work, because we’d be dividing by zero. When the normal to a plane is a null vector, there can be no reflections in that plane, because the normal vector itself will also lie in the plane, making it impossible for any element of O(2,1) to both preserve the plane and reverse the normal vector. The planes in 2+1 Minkowski space whose normal vectors are null are precisely those that are tangent to the light cone, and all of their vectors except those lying on the null ray shared with the light cone are spacelike. So if we choose two timelike vectors, the tangents to the world lines of tardyons, we will always be able to find a reflection in the plane they span.
Putting aside that exception, suppose we choose three linearly independent vectors u1, u2 and u3 such that none of the planes spanned by any pair of them is tangent to the light cone. We can then construct three elements of SO(2,1) as follows:
g1 = ref(u1, u2) ref(u1, u3)
g2 = ref(u2, u3) ref(u1, u2)
g3 = ref(u2, u3) ref(u1, u3)
We then have gi preserving ui for i=1,2,3, and g3 = g2g1. So if two particles with u1 and u2 as tangent vectors to their world lines collide, then they can give rise to an outgoing particle with u3 as the tangent to its world line, if the momenta of the three particles are such as to produce these gi as the Lorentz transformations around their world lines.
Apart from the exception previously noted, we can use this reflection-based construction to find collisions where the incoming and outgoing particles have any characteristics we like: each one can be a tardyon, a luxon or a tachyon. For example, suppose we want to find a collision in which two luxons coming from opposite directions collide and produce a tardyon, which in our chosen frame is moving at right angles to the luxons at 60% the speed of light. We set:
u1 = et + ex
u2 = et – ex
u3 = (5/4)et + (3/4)ey
We can then construct the three reflections and the three Lorentz transformations accordingly. To find the mass of the outgoing particle, we can compute the trace of g3, which turns out to be –429/625, and note that the trace of a rotation by an angle θ is 1+2cos(θ); this doesn’t completely pin down the rotation angle, but if we check g3 to see if its net rotation around u3 is clockwise or counter-clockwise we find that it’s counter-clockwise. So the rotation is by less than π, and we have:
m3 / mmax = arccos(–527/625) / (2π)
The vector-valued momentum of the outgoing particle in our chosen reference frame is then m3u3.
The Lorentz transformations associated with the two incoming luxons, g1 and g2, will be null rotations, i.e. transformations that preserve the null vectors u1 and u2 respectively. To find the vector-valued momenta that the incoming particles must have in order to yield the desired collision geometry, we need to think a bit more about the relationship between vector-valued and group-valued momenta.
One approach, described by John Baez in This Week’s Finds in Mathematical Physics, Week 232, is to pick an isomorphism L between the tangent space in 2+1 dimensions and the three-dimensional Lie algebra so(2,1), such that for any vector-valued momentum p, L(p) annihilates p. The Lorentz transformation associated with the particle with momentum p is then exp(k L(p)), which will preserve p. The constant k is chosen so that a tardyon of mass mmax produces a rotation of 2π.
Another approach is to require the group-valued momentum of a luxon to agree with that of a tardyon with close to the same momentum vector. Obviously no tardyon can ever have a null momentum vector, but if we consider tardyons of ever smaller mass moving ever faster, in the limiting case we should get the same results. A tardyon with a mass of λ√(1–v2) moving with an ordinary velocity vex will have a vector-valued momentum:
p = λ (et + vex)
which in the limit v→1 will be the null vector:
p0 = λ (et + ex)
If we compute the rotation around p by an angle 2πλ√(1–v2)/mmax, and take the limit as v→1, we get a null rotation which preserves the null vector p0; the precise element of SO(2,1) will depend only on λ. By solving for the value of λ that yields a given null rotation, such as g1, we can determine the vector-valued momentum associated with it.
Using this method for our two incoming luxons, we get:
2πλ1/mmax = 2πλ2/mmax = 6/5
with the vector-valued momenta of the luxons being λ1u1 and λ2u2.
For the sake of completeness, we should describe what happens if the momentum vectors of the two incoming particles in a collision span a plane with a null vector as its normal.
If we pick any null vector n, then the plane to which it is normal will include n itself, and also those spacelike vectors that lie in the plane tangent to the null cone along the null ray generated by n. A plane like this intersects the hyperboloid of unit spacelike vectors along two disjoint lines; the dot products of any of the vectors in one of these lines with another vector in the same line will always be 1, and with a vector in the other line will be –1.
The Lorentz transformations that preserve vectors in this plane constitute a subgroup of SO(2,1), so the momentum vector of the outgoing particle will also lie in the same plane. Despite the three vectors being coplanar, the outgoing momentum vector is not equal to the sum of the incoming momentum vectors, because the subgroup is not Abelian. However, the tachyonic masses associated with boosts that preserve these spacelike vectors are additive: if two tachyons with momenta in this plane collide, the mass of the outgoing tachyon will be the sum of the masses of the incoming ones. If the two momenta lie in opposite halves of the plane, which is divided in two by the null ray where it intersects the light cone, one mass will be subtracted from the other.
To see how this additive property arises, note that every boost has three real eigenvectors. As well as the spacelike vector that is preserved, the two null rays where the null cone intersects the plane orthogonal to the preserved vector are multiplied by eigenvalues exp(iπm/mmax) and exp(-iπm/mmax); these eigenvalues are real, because the mass of the tachyon is taken as imaginary to yield a consistent mathematical scheme where rotations by imaginary angles provide boosts. Now, if two different boosts have preserved vectors in the plane orthogonal to a null vector n, that null vector must be an eigenvector of both boosts. Consequently, n must be an eigenvector of their product, and its eigenvalue will be exp(±iπm1/mmax±iπm2/mmax). This also demonstrates closure of the subgroup under multiplication, because the vector preserved by the product of the boosts must be orthogonal to this null eigenvector.
|
|
|