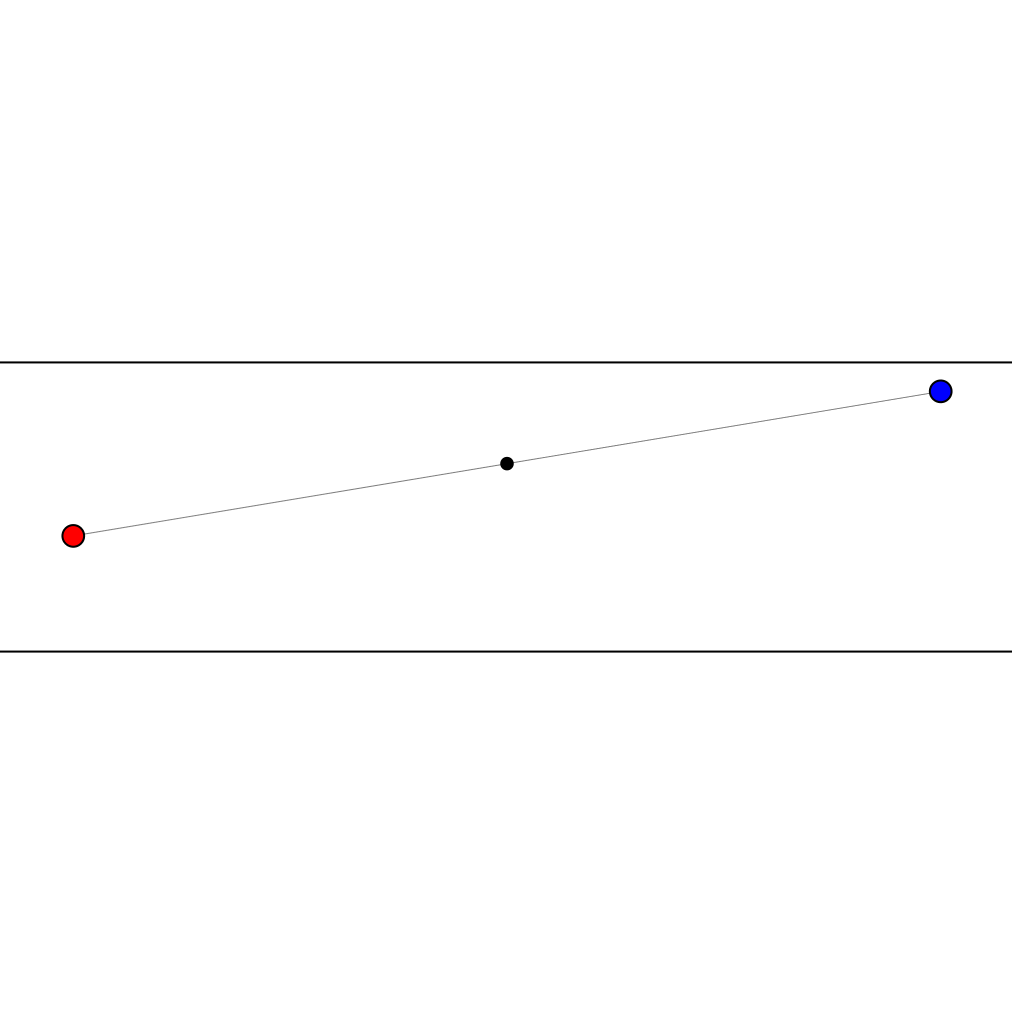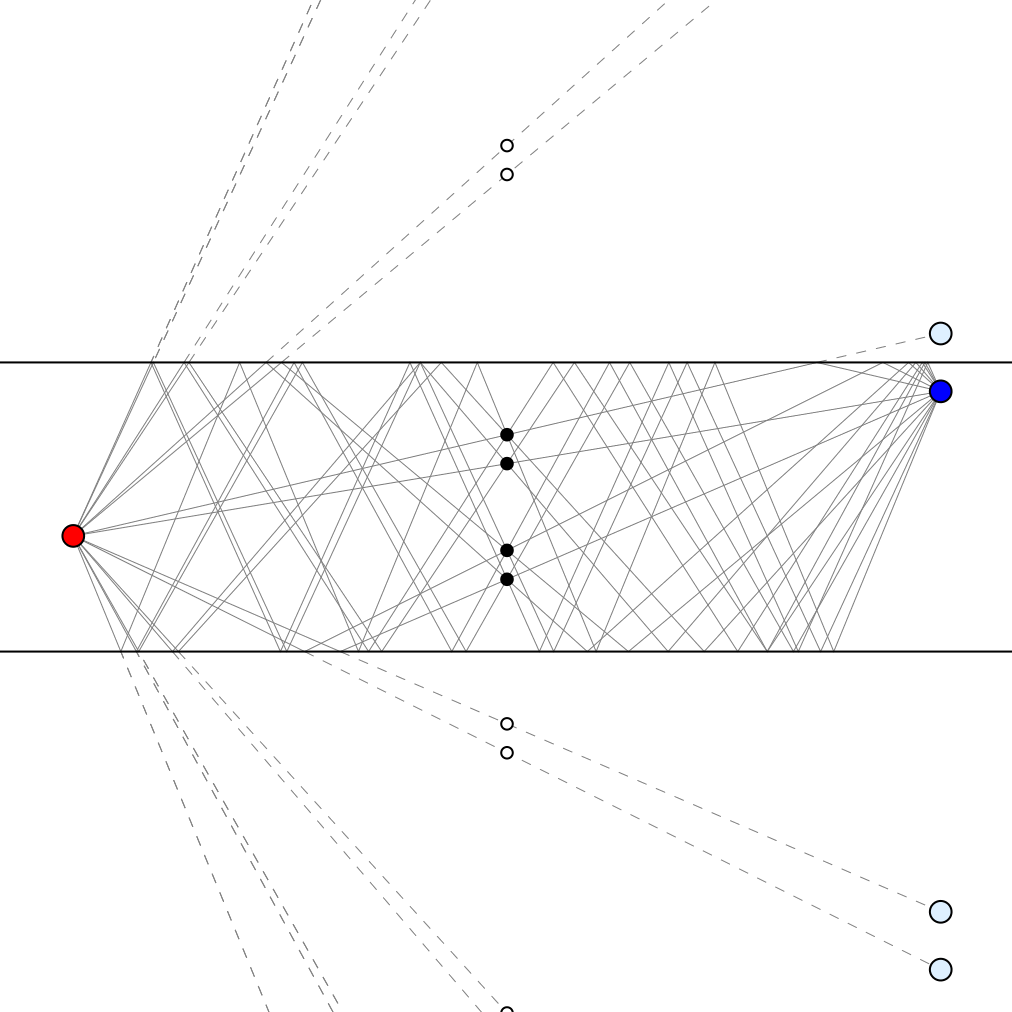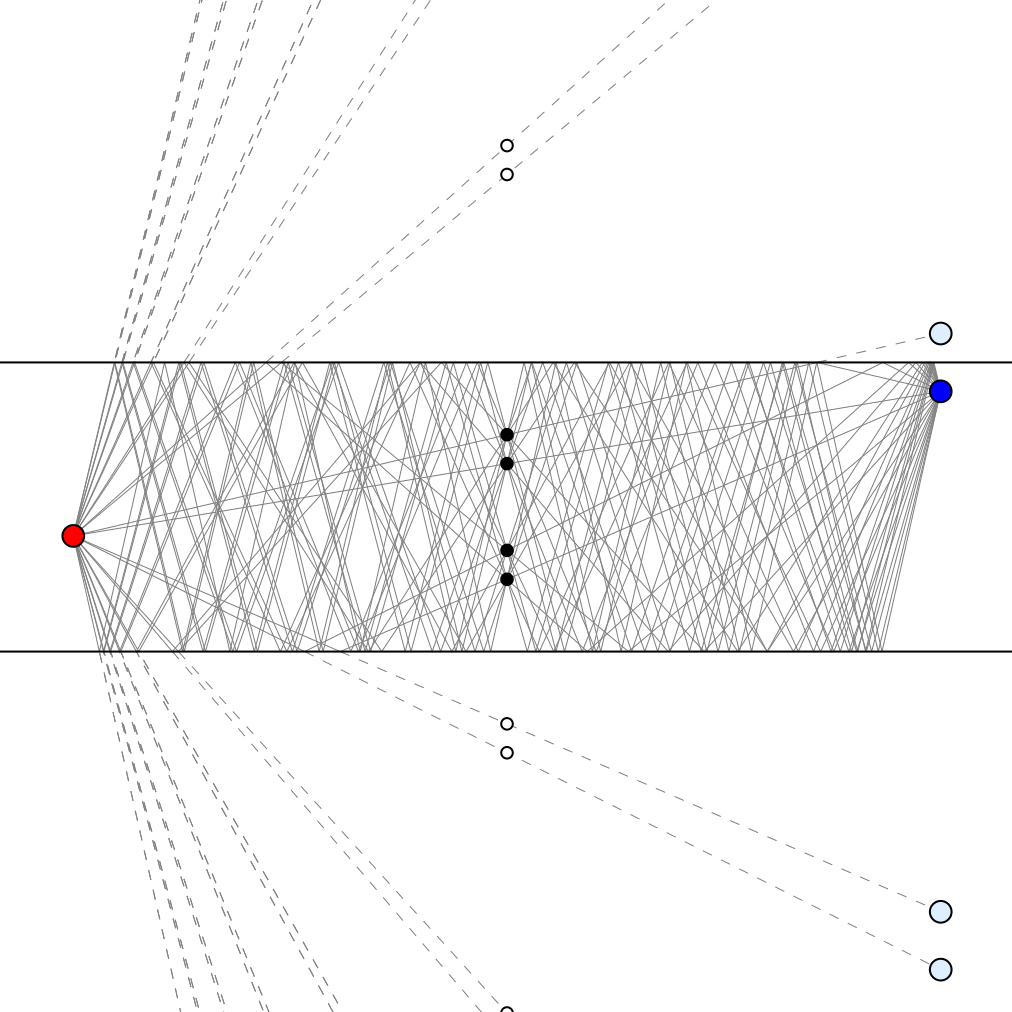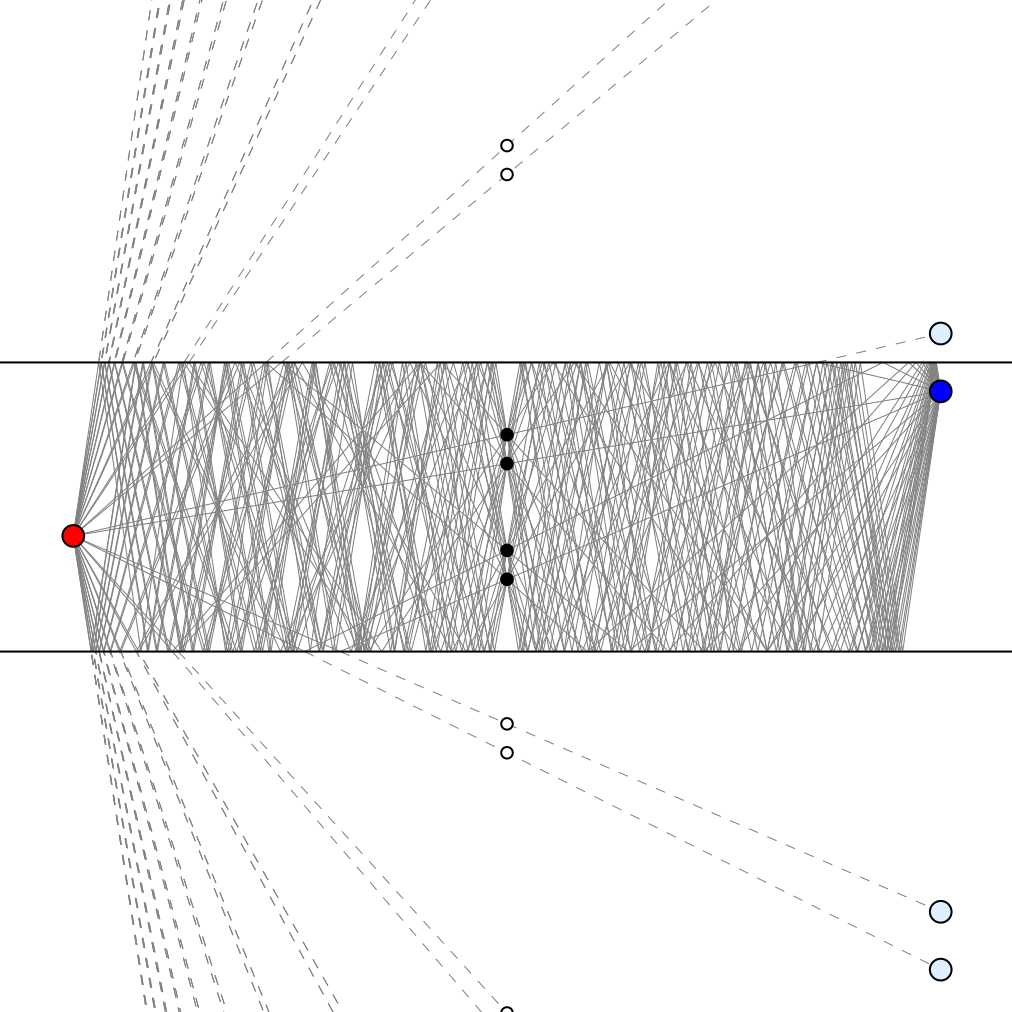
Given two points between two parallel mirrors (the red and blue dots in the animation on the left), there are an infinite number of light paths joining them, involving ever more reflections.
But all those paths can be blocked by obstructing just four points (the black dots).
The easiest way to see this is to note that the virtual images of the blue dot produced by the two mirrors (a few examples of which are shown here in light blue) consist of two equally spaced series of points, or 1-dimensional lattices. Reflecting in one mirror and then the other has a net effect of moving whatever is reflected by twice the distance between the mirrors, so all the images of the blue point (along with the actual blue point itself), form two equally spaced sets, with one set for an even number of reflections (including zero), and the other for an odd number of reflections.
For each 1-dimensional lattice, we can block all the paths from the red dot to the points in that lattice with just two obstacles. Why two? If the mirrors were not present and all the images in our chosen lattice were real objects, we could block the light paths to them by placing obstacles halfway between each of them and the red dot. But placing the obstacles halfway to a sequence of regularly spaced points means the obstacles themselves will also be regularly spaced, but with half the separation. So, we can place a single physical obstacle between the mirrors that will have the same effect as all the even-numbered virtual obstacles, and another that will have the same effect as all the odd-numbered virtual obstacles, since those subsets of the virtual obstacles each have the full spacing produced by a reflection in one mirror then the other.
Having dealt with the simplest example of this phenomenon, let’s see how it can be generalised to other arrangements of mirrors.
 |
 |
Suppose a celebrity is standing in a room with mirrored walls, and a paparazzo is in the same room. The paparazzo wants to photograph the celebrity, and by making use of the mirrored walls (and a powerful telephoto lens) they have an infinite number of possible directions in which they could point their camera and catch their target in exactly the centre of the frame.
But the celebrity is accompanied by a team of bodyguards, who will fearlessly employ their knowledge of geometry to position themselves to try to block the shots. With an infinite number of possible camera angles, can a finite number of bodyguards block every possible shot?
This is equivalent to a wonderful puzzle that was posed by the late Fields medalist Maryam Mirzakhani, and answered for the case of a square room by Emily Riehl, whose answer is beautifully described in this blog post by Tai-Danae Bradley.
It turns out that for a square room, once you fix the positions of the celebrity and the paparazzo, you can find positions for just 16 bodyguards that will block every possible shot!
The key to understanding this is to note that:
So, if you place bodyguards at each of the four points associated with each of the four lattices, you will be guaranteed to interrupt the light path for any possible shot.
Putting this into mathematical notation, suppose the celebrity’s physical location is c, and the paparazzos’s physical location is p. Call the basis vectors of the lattices a and b, so for a single lattice, images of the celebrity will appear at c + x a + y b for all integers x, y. The midpoints are then:
m(x, y) = (c + p + x a + y b)/2
There are an infinite number of such midpoints, but if we place bodyguards at the four points in the room:
B1 ~ (c + p)/2
B2 ~ (c + p)/2 + a/2
B3 ~ (c + p)/2 + b/2
B4 ~ (c + p)/2 + a/2 + b/2
then every midpoint in the infinite plane of images will differ from one of these by an integer multiple of lattice basis vectors, and so will correspond to the same physical point within the room.
Why have we written ~ (equivalent) here rather than an equals sign? The symbol ~ is used to mean “equal, up to the addition of some integer multiple of lattice basis vectors”. We don’t know that the vectors we have written on the right-hand sides of these equivalence relations actually lie within the room. But we do know that there will be locations in the room equivalent to these vectors.
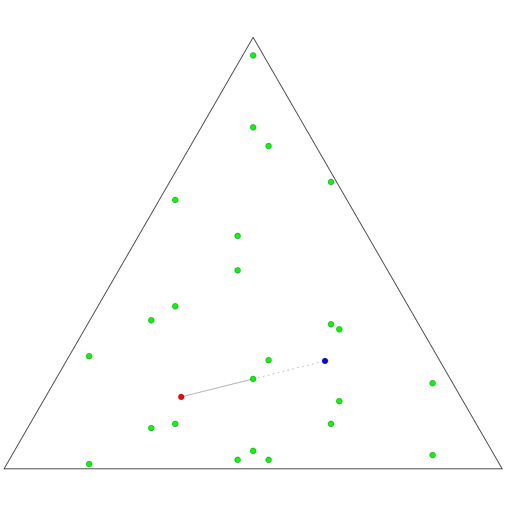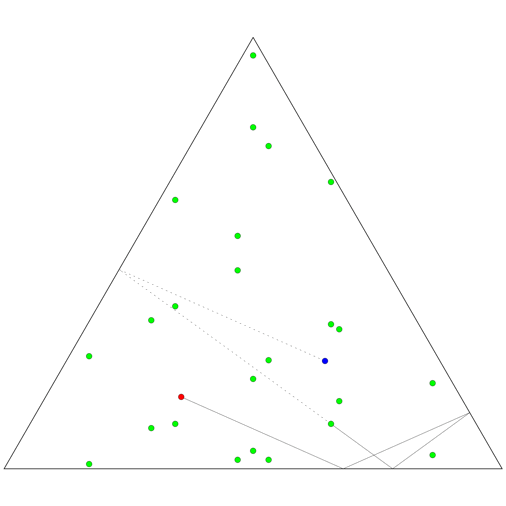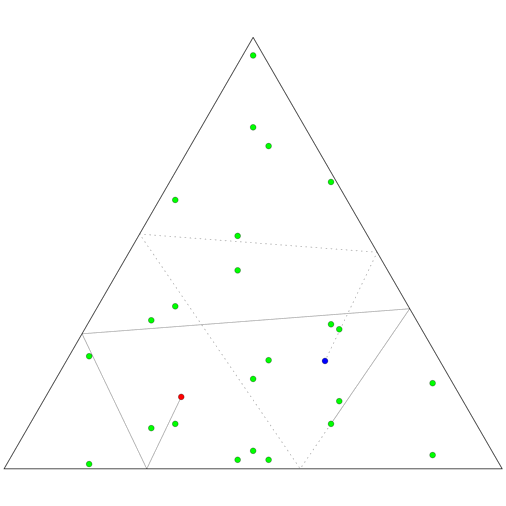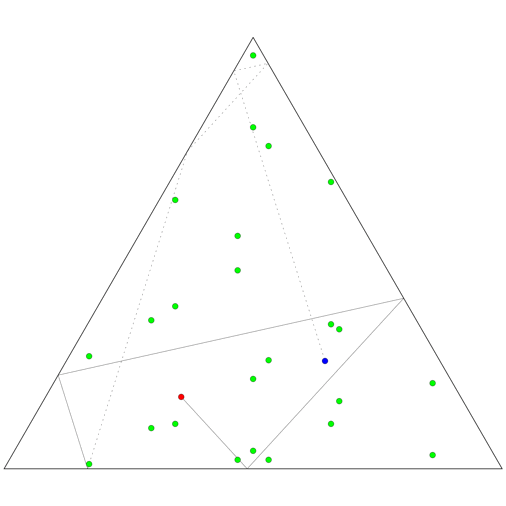
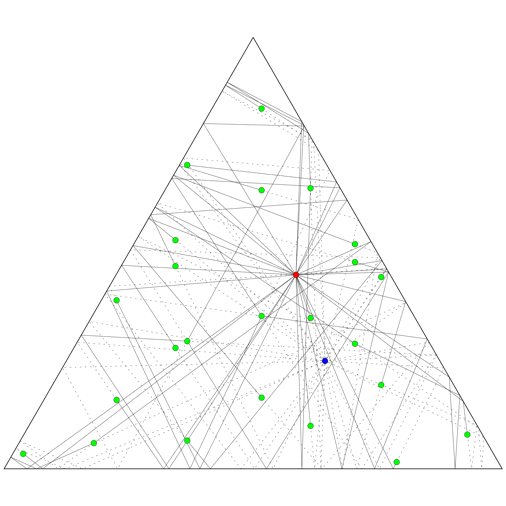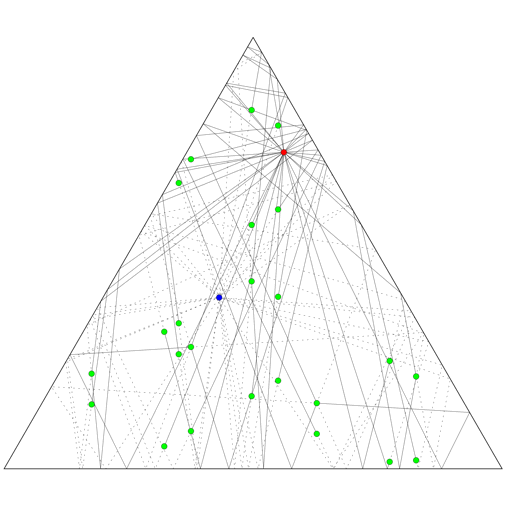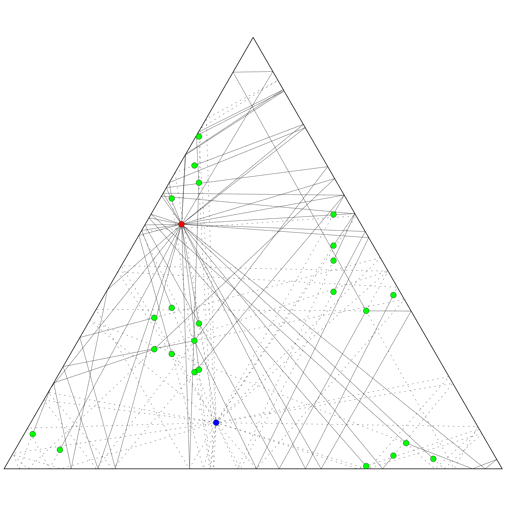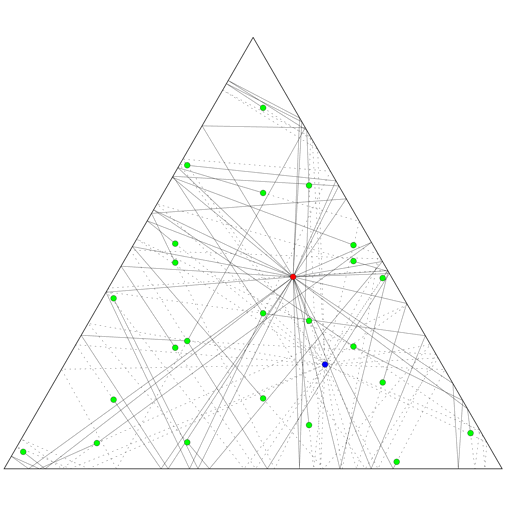
Now, what if the room is an equilateral triangle, rather than a square? It turns out that the set of images of the celebrity will be the union of six distinct lattices rather than four, so in total 24 bodyguards are needed.
The animation on the top right shows how 24 bodyguards (green) block various shots in a triangular room, for fixed positions of the celebrity (bue) and paparazzo (red), while the animation on the right shows how the bodyguards need to change position as the two move throughout the room.

The animation on the left shows the six lattices of images of a single point moving in a mirrored triangular room. The images of the room are given six distinct colours, depending on which lattice the image of the point they contain belongs to. The black parallelograms mark out domains of the lattices: regions of the plane that are identical, translated copies of each other. Where a domain starts and stops is arbitrary, depending on where we choose to place one corner of the parallelogram, while the size and direction of the sides is determined by the lattice. But all six of the lattices here are just translated copies of each other, so a single choice of domains applies to all of them.
Given a point in one of these domains, it might lie inside a triangle of any of the six colours. But if we pick one triangle (say the yellow one at the centre) to represent the physical room, there is a unique identification between that triangle and any of the others, which we can make by repeatedly reflecting the yellow triangle in each of its mirrored walls.
 |
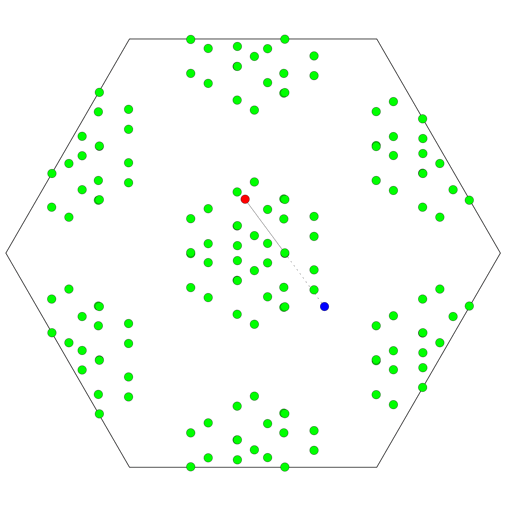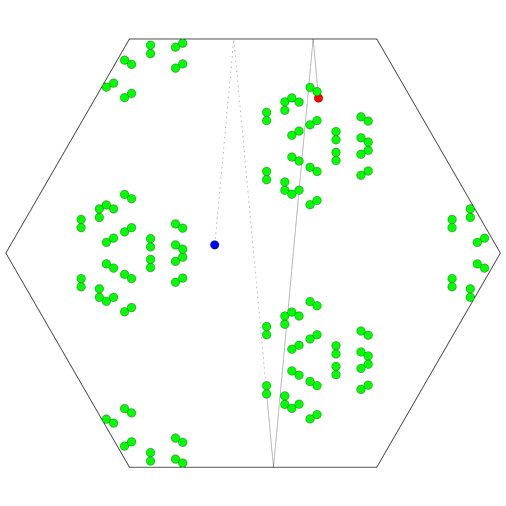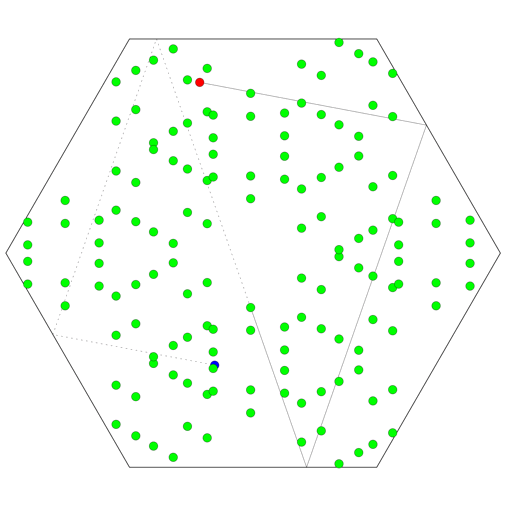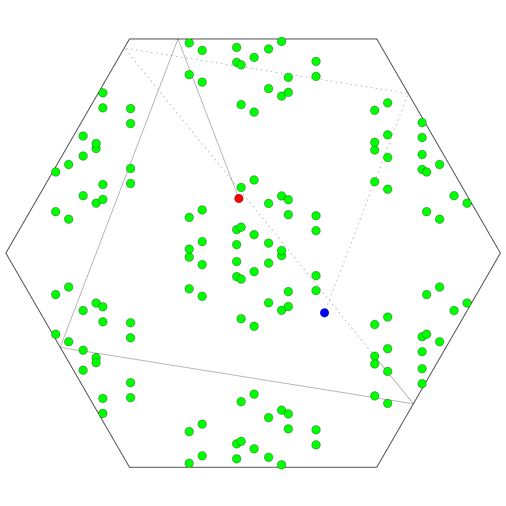 |
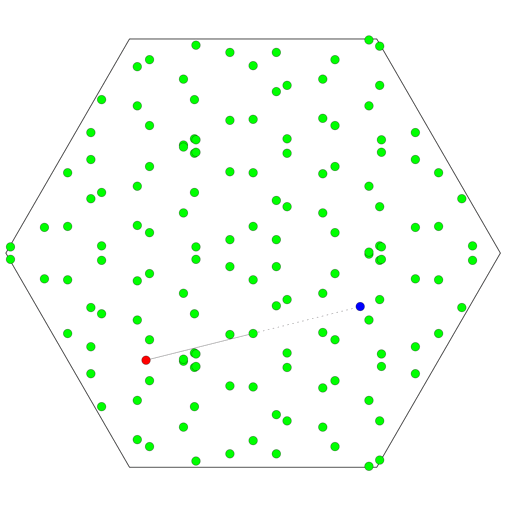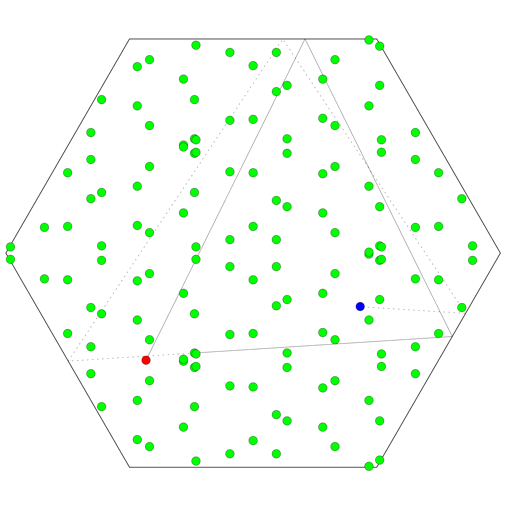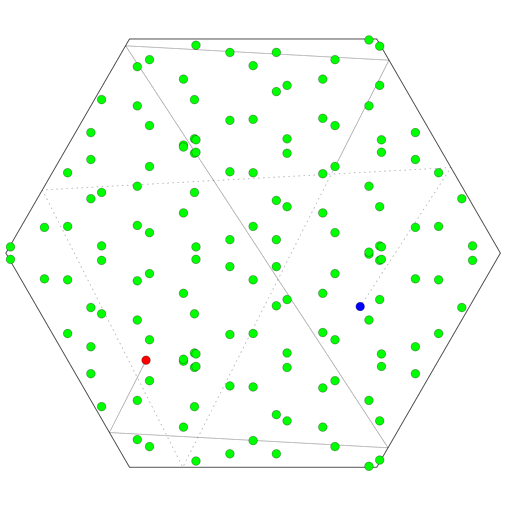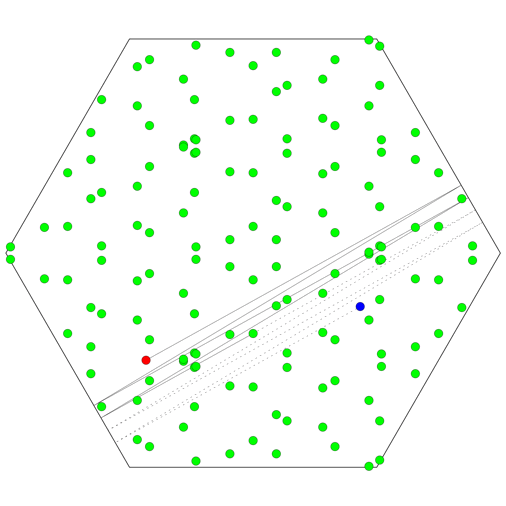
What if the room is a regular hexagon? Again, the set of images of the celebrity will be the union of six distinct lattices, but there is a further twist. The 24 midpoints that are all equivalent modulo translations in the lattice can each correspond to any of 6 different physical locations within the hexagon, so a total of 144 bodyguards are needed!
Why is there such a pronounced difference from the square and triangular cases? If you tile the plane with regular hexagons, three of the hexagons meet at each corner. This is an odd number, unlike the four that meet at each corner in a square tiling, or the six in a triangular tiling. If you follow the reflections around each corner, the odd number of reflections means that the virtual image of the original object will not be overlayed on its original position; rather, the whole image of the room will be mirror-reversed.
All in all, there can be up to 6 images of the object within a single image of the room. Of course, no single sequence of reflections can make a room containing only one object appear to contain six copies of that object! But the same virtual room in the tiled plane can be seen by multiple routes: different sequences of reflections that end up rotating and/or reflecting the room differently. So instead of having a unique way to identify any hexagon with any other, there are 6 distinct possibilities that depend on the particular sequence of reflections involved. And since the paparazzo might make use of any of these possibilities, the number of bodyguards required is multiplied by an extra factor of 6.
(Note that the animation below shows the complete, idealised set of points, regardless of whether or not they would actually be visible to anyone. The true set of images that a given observer would be able to see at any moment would be some subset of this.)

|
|
|